题目内容
【题目】如图所示，在圆形区域内，存在垂直纸面向外的匀强磁场，ab是圆的一条直径．一带正电的粒子从a点射入磁场，速度大小为2v，方向与ab成30°时恰好从b点飞出磁场，粒子在磁场中运动的时间为t；若仅将速度大小改为v，则粒子在磁场中运动的时间为（不计带电粒子所受重力）（ ）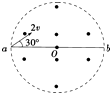
A.3t
B.
t
C.
t
D.2t
【答案】D
【解析】解：设磁场圆的半径为R，根据周期公式T= 
可得，同一粒子在磁场中运动时的运动的周期相同，
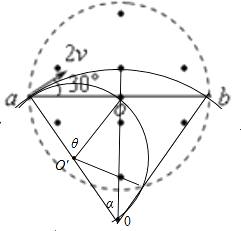
当速度的大小为2v时，圆周运动的圆心为O，根据弦切角等于圆心角的一半可知，圆弧所对的圆心角为60°；
磁场圆的半径恰好是粒子圆周运动半径的一半；
当速度的大小为v时，半径为原来的一半，圆周运动的圆心O′点，在原来的半径的中点处，
则新的粒子圆与磁场圆的半径相等，则θ=60°；由几何关系可知所对的圆心角为120°，
则粒子的运动的时间为2t，故D正确；
故选：D．
练习册系列答案
相关题目
