题目内容
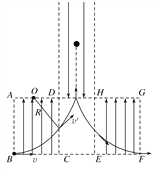
【题目】如图所示,两个边长均为l的正方形区域ABCD和EFGH内有竖直向上的匀强电场,DH上方有足够长的竖直向下的匀强电场.一带正电的粒子,质量为m,电荷量为q,以速度v从B点沿BC方向射入匀强电场,已知三个区域内的场强大小相等,且![]() ,今在CDHE区域内加上合适的垂直纸面向里的匀强磁场,粒子经过该磁场后恰能从DH的中点竖直向上射入电场,粒子的重力不计,求:
,今在CDHE区域内加上合适的垂直纸面向里的匀强磁场,粒子经过该磁场后恰能从DH的中点竖直向上射入电场,粒子的重力不计,求:

(1)所加磁场的宽度DH;
(2)所加磁场的磁感应强度大小;
(3)粒子从B点射入到从EFGH区域电场射出所经历的总时间.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)粒子在ABCD区域电场中做类平抛运动,射出该电场时沿电场方向偏转距离为d
由Eq=ma得a=![]()
由l=vt得t=![]()
故d=![]() at2=
at2=![]() l
l
粒子射出ABCD区域电场时沿场强方向速度为vy=at=v
速度偏向角为tanθ=![]() =1
=1
解得θ=![]()
粒子从DH中点竖直向上射入电场,由几何关系知
![]()
![]()
得![]() 得
得![]()
(2)射入磁场的速度大小为v′=![]() v
v
由洛伦兹力提供向心力qv′B=m![]()
解得B=![]()
(3)粒子在左侧电场中偏转的运动时间t1=![]()
粒子在磁场中向上偏转运动时间t2=![]() T
T
其中T=![]()
在上方电场中运动减速到零的时间为t3=![]()
粒子运动轨迹如图所示,根据对称性可知粒子运动总时间为
t=2(t1+t2+t3)
得![]() 或t=
或t=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目