题目内容
2.同重力场作用下的物体具有重力势能一样,万有引力场作用下的物体同样具有引力势能.若取无穷远处引力势能为零,物体距星球球心距离为r时的引力势能为Ep=-G$\frac{{m}_{0}m}{r}$(G为引力常量、m0为星球质量),设宇宙中有一个半径为R的星球,宇航员在该星球上以初速度v0竖直向上抛出一个质量为m的物体,不计空气阻力,经t秒后物体落回手中,则以下说法错误的是( )| A. | 在该星球表面上以$\sqrt{\frac{2{v}_{0}R}{t}}$的初速度水平抛出一个物体,物体将不再落回星球表面 | |
| B. | 在该星球表面上以2$\sqrt{\frac{{v}_{0}R}{t}}$的初速度水平抛出一个物体,物体将不再落回星球表面 | |
| C. | 在该星球表面上以2$\sqrt{\frac{{v}_{0}R}{t}}$的初速度竖直抛出一个物体,物体将不再落回星球表面 | |
| D. | 在该星球表面上以 $\sqrt{\frac{2{v}_{0}R}{t}}$的初速度竖直抛出一个物体,物体将不再落回星球表面 |
分析 物体做竖直上抛运动,根据物体的运动时间,求出星球表面的重力加速度;卫星绕星球表面做圆周运动,万有引力提供向心力,由牛顿第二定律可以求出水平抛出的速度;将物体竖直上抛时,卫星机械能守恒,由机械能守恒定律可以求出竖直上抛的速度.
解答 解:A、物体做竖直上抛运动,则有:v0=g×$\frac{t}{2}$,
解得星球表面重力加速度为:g=$\frac{{2v}_{0}}{t}$,
设星球半径为R,卫星绕星球表面做圆周运动,万有引力等于重力提供向心力:m$\frac{{v}^{2}}{R}$=mg,
解得:v=$\sqrt{gR}$=$\sqrt{\frac{2{v}_{0}R}{t}}$,此为最大的环绕速度,也是最小的发射速度,
故以此速度或超过此速度水平抛出,都不会落回地面,故AB正确;
C、若竖直上抛,设速度为v′时,卫星绕星球表面运动时,由机械能守恒定律得:
-G$\frac{mM}{R}$+$\frac{1}{2}$mv′2=0,
又$\frac{GMm}{{R}^{2}}$=mg,
解得:v′=2$\sqrt{\frac{{v}_{0}R}{t}}$,故C正确,D错误;
本题选错误的,故选:D
点评 熟练应用竖直上抛运动运动规律、知道发射卫星时机械能守恒,是正确解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
12.根据《中国广播电视报》报道,在暑天就诊的小病人,低锌发病率高达60%以上.由于锌对人体代谢起着重要作用,因此儿童生长发育时期测量体内含锌量已成为体格检查的重要内容之一,也引起了我国科技工作者的高度重视.其中比较简单的一种检测方法是取儿童的头发约50g,放在核反应堆中经中子轰击后,头发中的锌元素与中子反应生成具有放射性的同位素锌,其核反应方程式为${\;}_{30}^{64}$Zn+${\;}_{0}^{1}$n→${\;}_{30}^{65}$Zn.${\;}_{30}^{65}$Zn衰变放射出能量为1115eV的γ射线,通过测定γ射线的强度可以计算出头发中锌的含量.关于以上叙述,下列说法正确的是( )
| A. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn有相同的核子数 | |
| B. | ${\;}_{30}^{64}$Zn和${\;}_{30}^{65}$Zn具有相同的质子数 | |
| C. | γ射线具有很强的穿透能力,能穿透几厘米的铅板 | |
| D. | γ射线在真空中传播的速度是3.0×108m/s |
7. 如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下以顺时针方向以Q点为焦点的椭圆运动,线段MN为椭圆的长轴,则电子在运动过程中( )
如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下以顺时针方向以Q点为焦点的椭圆运动,线段MN为椭圆的长轴,则电子在运动过程中( )
 如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下以顺时针方向以Q点为焦点的椭圆运动,线段MN为椭圆的长轴,则电子在运动过程中( )
如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下以顺时针方向以Q点为焦点的椭圆运动,线段MN为椭圆的长轴,则电子在运动过程中( )| A. | 在M点的速率最小 | |
| B. | 在电子从M点向N点运动过程中电势能减小 | |
| C. | 电子从N点向M点运动库仑力做负功 | |
| D. | 电子在椭圆上经过N点时所受电场力最小 |
14. 如图所示,光滑绝缘水平桌面上直立一个单匝矩形导线框,线框的边长LAB=0.3m,LAD=0.2m,总电阻为R=0.1Ω.在直角坐标系xOy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=0.2sin$\frac{10π}{3}$x(m),磁感应强度大小B=0.2T.线框在沿x轴正方向的拉力F作用下,以速度v=10m/s水平向右做匀速直线运动,则下列判断正确的是( )
如图所示,光滑绝缘水平桌面上直立一个单匝矩形导线框,线框的边长LAB=0.3m,LAD=0.2m,总电阻为R=0.1Ω.在直角坐标系xOy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=0.2sin$\frac{10π}{3}$x(m),磁感应强度大小B=0.2T.线框在沿x轴正方向的拉力F作用下,以速度v=10m/s水平向右做匀速直线运动,则下列判断正确的是( )
 如图所示,光滑绝缘水平桌面上直立一个单匝矩形导线框,线框的边长LAB=0.3m,LAD=0.2m,总电阻为R=0.1Ω.在直角坐标系xOy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=0.2sin$\frac{10π}{3}$x(m),磁感应强度大小B=0.2T.线框在沿x轴正方向的拉力F作用下,以速度v=10m/s水平向右做匀速直线运动,则下列判断正确的是( )
如图所示,光滑绝缘水平桌面上直立一个单匝矩形导线框,线框的边长LAB=0.3m,LAD=0.2m,总电阻为R=0.1Ω.在直角坐标系xOy中,有界匀强磁场区域的下边界与x轴重合,上边界满足曲线方程y=0.2sin$\frac{10π}{3}$x(m),磁感应强度大小B=0.2T.线框在沿x轴正方向的拉力F作用下,以速度v=10m/s水平向右做匀速直线运动,则下列判断正确的是( )| A. | 线框中的电流先沿逆时针方向再沿顺时针方向 | |
| B. | 线框中感应电动势的最大值为0.4V | |
| C. | 线框中感应电流有效值为4A | |
| D. | 线框穿过磁场区域的过程中外力做功为0.024J |
11.在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图甲所示,并在其上取了A、B、C、D、E、F、G 7个计数点,每相邻两个计数点间还有4个点图中没有画出,他们相邻之间的间距分别为d1,d2,d3,d4,d5,d6.电火花计时器接220V、50Hz交流电源.他经过测量并计算得到电火花计时器在
打B、C、D、E、F各点时物体的瞬时速度如表:

(1)设电火花计时器的周期为T,计算vF的公式为vF=$\frac{{d}_{6}-{d}_{4}}{10T}$;
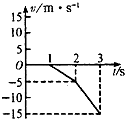
(2)根据(1)中得到的数据,以A点对应的时刻为t=0,试在图乙所示坐标系中合理地选择标度,作出v-t图象.
(3)利用该图象求物体的加速度a=0.4m/s2;
(4)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比不变(选填:“偏大”、“偏小”或“不变”).
打B、C、D、E、F各点时物体的瞬时速度如表:
| 对应点 | B | C | D | E | F |
| 速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |

(1)设电火花计时器的周期为T,计算vF的公式为vF=$\frac{{d}_{6}-{d}_{4}}{10T}$;
(2)根据(1)中得到的数据,以A点对应的时刻为t=0,试在图乙所示坐标系中合理地选择标度,作出v-t图象.
(3)利用该图象求物体的加速度a=0.4m/s2;
(4)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比不变(选填:“偏大”、“偏小”或“不变”).
12. 两个相同的条形磁铁,放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁皆处于水平位置,且静止不动.现将AB突然竖直向下平移(磁铁与平板间始终相互接触),并使之停在A′B′处,结果发现两个条形磁铁碰在一起.以下说法正确的是( )
两个相同的条形磁铁,放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁皆处于水平位置,且静止不动.现将AB突然竖直向下平移(磁铁与平板间始终相互接触),并使之停在A′B′处,结果发现两个条形磁铁碰在一起.以下说法正确的是( )
 两个相同的条形磁铁,放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁皆处于水平位置,且静止不动.现将AB突然竖直向下平移(磁铁与平板间始终相互接触),并使之停在A′B′处,结果发现两个条形磁铁碰在一起.以下说法正确的是( )
两个相同的条形磁铁,放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁皆处于水平位置,且静止不动.现将AB突然竖直向下平移(磁铁与平板间始终相互接触),并使之停在A′B′处,结果发现两个条形磁铁碰在一起.以下说法正确的是( )| A. | AB竖直向下平移到停在A′B′处过程中,磁铁对板的压力大于磁铁的重力 | |
| B. | AB竖直向下平移到停在A′B′处过程中,磁铁对板的压力小于磁铁的重力 | |
| C. | 如果将AB从原位置突然竖直向上平移,并使之停在A″B″位置处,两条形磁铁一定不可能碰在一起 | |
| D. | 如果将AB从原位置突然竖直向上平移,并使之停在A″B″位置处,两条形磁铁也有可能碰在一起 |
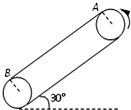 如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度?
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度? 如图甲所示.在倾角为30°的足够长的光滑斜面上有一个质量为m的物体,它受到沿斜面方向的力F的作用.力F按图乙所示的方式随时间变化(图中纵坐标是F与mg的比值,力F沿斜面向上为正).已知重力加速度g=10m/s2,此物体在t=0时的速度为零.则关于物体的速度随时间变化的关系图象,下列正确的是( )
如图甲所示.在倾角为30°的足够长的光滑斜面上有一个质量为m的物体,它受到沿斜面方向的力F的作用.力F按图乙所示的方式随时间变化(图中纵坐标是F与mg的比值,力F沿斜面向上为正).已知重力加速度g=10m/s2,此物体在t=0时的速度为零.则关于物体的速度随时间变化的关系图象,下列正确的是( )