��Ŀ����
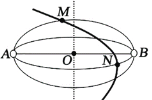
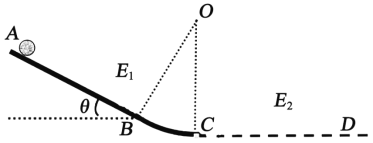
����Ŀ����ͼ��ʾ���ռ��д�������ˮƽ�����![]() �Ĺ⻬б����AB��Բ����O��Ĺ⻬Բ�����BC�������������B�㣬Բ���뾶ΪR��AB��
�Ĺ⻬б����AB��Բ����O��Ĺ⻬Բ�����BC�������������B�㣬Բ���뾶ΪR��AB��![]() ����OCΪ�߽��Ϊ���������֣�����OC��ߣ���OC�ߣ�������ǿ�糡E1��OC�ұߴ�����ǿ�糡E2.����ǿE1�ķ���ˮƽ����ʱ���ڹ����A�������ͷ�һ����Ϊm�������Ϊq�Ĵ�����С��С��ǡ����A�㱣�־�ֹ��������ǿE1����ı�Ϊ��ֱ���º�С���ع����C��ˮƽ�ɳ���������ǿ�糡E2�С�С����E2����ˮƽֱ��CD�˶�����Զ������C�����
����OCΪ�߽��Ϊ���������֣�����OC��ߣ���OC�ߣ�������ǿ�糡E1��OC�ұߴ�����ǿ�糡E2.����ǿE1�ķ���ˮƽ����ʱ���ڹ����A�������ͷ�һ����Ϊm�������Ϊq�Ĵ�����С��С��ǡ����A�㱣�־�ֹ��������ǿE1����ı�Ϊ��ֱ���º�С���ع����C��ˮƽ�ɳ���������ǿ�糡E2�С�С����E2����ˮƽֱ��CD�˶�����Զ������C�����![]() ��D�㡣����֪�������ٶ�Ϊg��
��D�㡣����֪�������ٶ�Ϊg��![]() ��
��![]() ����
����
(1)�糡ǿ��E1�Ĵ�С��
(2)С��C��ʱ�Թ����ѹ����
(3)��ǿE2�Ĵ�С�ͷ���
���𰸡�(1)![]() ��(2) 5.95 mg��������ֱ���£�(3)
��(2) 5.95 mg��������ֱ���£�(3)![]() �� ������ˮƽ�����
�� ������ˮƽ�����![]() ��б�����Ϸ�
��б�����Ϸ�
��������
(1)��A��ƽ��ʱ����������ͼ
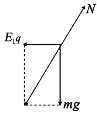
�ɼ��ι�ϵ��
![]()
���
![]()
(2)�ı�E1�����С����A��C�Ĺ������ɶ��ܶ����ɵ�
![]()
��C������������
![]()
���
N = 5.95 mg
��ţ�ٵ������ɿ�֪��
F = N = 5.95 mg
������ֱ���¡�
(3)����糡E2�����ȼ���ֱ���˶������ȱ��ٹ�ʽ��
![]()
���
a = g
��С���������������ͼ
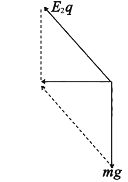
�ɼ��ι�ϵ�ɵ�
![]()
���
![]()
������ˮƽ�����![]() ��б�����Ϸ�
��б�����Ϸ�

 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�