题目内容
13．
如图所示．两个相同的小球A、B用长均为0.8m的细绳悬于小车顶部，随小车一起向右匀速运动，速度为4m/s，两球与小车前后壁接触，若某时刻小车突然停止运动，则此时悬线的拉力之比为FA：FB为（ ）（重力加速度g取10m/s2）| A． | 2：1 | B． | 3：1 | C． | 1：2 | D． | 1：3 |
分析 小车突然停止运动，A球由于惯性，会向前摆动，将做圆周运动，B球受到小车前壁的作用停止运动，在竖直方向上拉力等于重力，根据牛顿第二定律求出A球绳的拉力，从而求出两悬线的拉力之比．
解答 解：若A、B的质量为m，则
对A球有：${F}_{A}-mg=m\frac{{v}^{2}}{L}$，
解得：${F}_{A}=mg+m\frac{{v}^{2}}{L}=10m+20m=30m$．
对B球有：FB=mg=10m．
所以FA：FB=3：1．
故选：B．
点评 解决本题的关键知道小车刹车后，A球将做圆周运动，最低点，重力和拉力的合力提供向心力．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3．
土星已确认有10颗卫星，其中土卫一与土星距离约为19万千米，土卫五与土星距离约为53万千米，如图，土卫一和土卫五绕土星可近似看做匀速圆周运动，则以下说法正确的是（ ）
土星已确认有10颗卫星，其中土卫一与土星距离约为19万千米，土卫五与土星距离约为53万千米，如图，土卫一和土卫五绕土星可近似看做匀速圆周运动，则以下说法正确的是（ ）| A． | 土卫五的周期大于土卫一的周期 | |
| B． | 土卫五的线速度大于土卫一的线速度 | |
| C． | 土卫五的角速度大于土卫一的角速度 | |
| D． | 土卫五的向心加速度大于土卫一的向心加速度 |
如图所示，光滑水平面上有一质量为M、长为L的长木板，上表面水平粗糙，一可视为质点的质量为m的滑块静止在长木板左端，给滑块一个瞬时冲量使其获得向右的初速度V，滑块恰好到达长木板右端并相对长木板静止（重力加速度为g）．求：
1．
如图所示，固定在同一水平面内的两根平行长直金属导轨的间距为d，其右端接有阻值为R的电阻，整个裝置处在竖直向上磁感应强度大小为B的匀强磁场中．一质量为m的均匀导体杆ab垂直于导轨放置，且与两导轨保持良好接触，ab杆长与导轨间距相同，杆与导轨之间的动摩擦因数为μ．当杆ab在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时，速度恰好达到最大（运动过程中始终与导轨保持垂直）．设杆的电阻为r，导轨电阻不计，重力加速度为g．则在此过程中（ ）
如图所示，固定在同一水平面内的两根平行长直金属导轨的间距为d，其右端接有阻值为R的电阻，整个裝置处在竖直向上磁感应强度大小为B的匀强磁场中．一质量为m的均匀导体杆ab垂直于导轨放置，且与两导轨保持良好接触，ab杆长与导轨间距相同，杆与导轨之间的动摩擦因数为μ．当杆ab在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时，速度恰好达到最大（运动过程中始终与导轨保持垂直）．设杆的电阻为r，导轨电阻不计，重力加速度为g．则在此过程中（ ）| A． | 杆的速度最大值为$\frac{F（R+r）}{{B}^{2}{d}^{2}}$ | |
| B． | 流过电阻R的电荷量为$\frac{BdL}{（R+r）}$ | |
| C． | 恒力F做的功大于回路中产生的电热与杆动能的变化量之和 | |
| D． | 恒力F做的功等于回路中产生的电热与杆动能的变化量之和 |
18．
如图所示，A、B、C三个物体材料相同，均放在旋转的水平圆台上，A、B的质量均为m，C的质量为2m，A、C离轴的距离均为2R，B离轴的距离为R，则当圆台旋转时（A、B、C均未滑动），以下说法正确的是（ ）
如图所示，A、B、C三个物体材料相同，均放在旋转的水平圆台上，A、B的质量均为m，C的质量为2m，A、C离轴的距离均为2R，B离轴的距离为R，则当圆台旋转时（A、B、C均未滑动），以下说法正确的是（ ）| A． | B的向心加速度最小 | B． | C的向心加速度最小 | ||
| C． | 当圆台转速增加时，C比B先滑动 | D． | 当圆台转速增加时，B比A先滑动 |
5．发现万有引力定律与测定万有引力常量的科学家分别是（ ）
| A． | 牛顿卡文迪许 | B． | 开普勒牛顿 | C． | 牛顿伽利略 | D． | 伽利略第谷 |
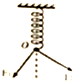如图所示，一端固定在轻质弹簧处于原长，现用相互垂直的两个力F1、F2拉弹簧的另一端至O点，在此过程F1、F2分别做了6J、8J的功，则弹簧的弹性势能为（ ）