题目内容
4. 如图所示,光滑水平面上有一质量为M、长为L的长木板,上表面水平粗糙,一可视为质点的质量为m的滑块静止在长木板左端,给滑块一个瞬时冲量使其获得向右的初速度V,滑块恰好到达长木板右端并相对长木板静止(重力加速度为g).求:
如图所示,光滑水平面上有一质量为M、长为L的长木板,上表面水平粗糙,一可视为质点的质量为m的滑块静止在长木板左端,给滑块一个瞬时冲量使其获得向右的初速度V,滑块恰好到达长木板右端并相对长木板静止(重力加速度为g).求:(1)滑块到在长木板右端时的速度;
(2)滑块与长木板上表面之间的动摩擦因数μ.
分析 (1)对两物体进行分析,根据动量守恒定律可求得共同的速度;
(2)在整个滑动过程中只有摩擦力做功;根据功能关系可求得动摩擦因数.
解答 解:规定向右为正方向
(1)滑块从左到右过程系统动量守恒,有:
mv=(M+m)V1
得:V1=$\frac{mv}{M+m}$
(2)滑块从左到右过程只有滑动摩擦力做负功,根据能的转换与守恒定律有:
μmgL=$\frac{1}{2}$mv2-$\frac{1}{2}$(M+m)v12
解得:μ=$\frac{M{v}^{2}}{2gL(M+m)}$
答:(1)滑块到在长木板右端时的速度为$\frac{mv}{M+m}$
(2)滑块与长木板上表面之间的动摩擦因数μ为$\frac{M{v}^{2}}{2gL(M+m)}$.
点评 本题考查动量守恒定律及功能关系的应用,要注意明确动量守恒的条件,同时注意动量守恒定律中的方向性;要明确正方向.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
14. 如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
 如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )
如图所示,匀强电场中有一圆,其所在平面与电场线平行,O为圆心,A、B、C、D为圆周上的四个等分点.若将某带电粒子从A点以相同的初动能向各个不同的方向发射,到达圆周上各点时,过D点动能最大,不计重力和空气阻力.则( )| A. | 该电场的电场线一定与OD平行 | |
| B. | 该带电粒子一定带正电 | |
| C. | 带电粒子若经过C点,则其动能不可能与初动能相同 | |
| D. | 带电粒子不可能经过B点 |
12.两个质量不同的物体,以相同的动能从地面竖直向上抛出(不计空气阻力),选地面为零势能面,当两物体上升到同一高度是,它们( )
| A. | 具有的重力势能相等 | B. | 具有的动能相等 | ||
| C. | 具有的机械能相等 | D. | 具有的机械能不相等 |
19.大气气流的升降运动会造成不同高度的温度变化,致使气象万变,万米高空的气温往往在-50℃以下,在研究大气现象时可反温度、压强相同的一部分气体人为研究对象,叫做气团,气团直径可达几千米,由于气团很大,边缘部分与外界的热交换对使个气团没有明显影响,可以忽略,用气团理论解释高空气温很低的原因,是因为地面的气团上升到高空的过程中( )
| A. | 剧烈膨胀,同时大量对外放热,使周围温度降低 | |
| B. | 剧烈收缩,同时从周围吸收大量热量,使周围温度降低 | |
| C. | 剧烈膨胀,气团对外做功,内能大量减少导致温度降低 | |
| D. | 剧烈收缩,外界对气团做功,故周围温度降低 |
 如图,ABCD轨道固定在竖直平面内,AB是半径R1=1m的四分之一圆弧轨道,与水平面相切与B点,CD是半径R2=0.5m光滑半圆轨道,与水平面相切与C点,BC段动摩擦因数μ=0.3.现一可视为质点的小球,从距离A点正上方高H=2m的O点静止释放后,恰沿A点进入轨道,通过B点时的速度为7m/s,已知小球质量m=0.2kg,不计空气阻力,g=10m/s2求:
如图,ABCD轨道固定在竖直平面内,AB是半径R1=1m的四分之一圆弧轨道,与水平面相切与B点,CD是半径R2=0.5m光滑半圆轨道,与水平面相切与C点,BC段动摩擦因数μ=0.3.现一可视为质点的小球,从距离A点正上方高H=2m的O点静止释放后,恰沿A点进入轨道,通过B点时的速度为7m/s,已知小球质量m=0.2kg,不计空气阻力,g=10m/s2求: 如图所示,质量为m=2kg的小物块从倾角θ=37°的光滑斜面上的A点由静止
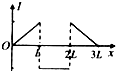
如图所示,质量为m=2kg的小物块从倾角θ=37°的光滑斜面上的A点由静止 如图所示,等腰三角形内以底边中垂线为界,两边分布有垂直纸面、磁感应强度大小相同且方向相反的匀强磁场,三角形高为L,长为2L,底边在x轴上.一边长为L的正方形导线框在纸面内沿x轴正方向匀速穿过匀强磁场区域,在t=0时刻恰好位于图中所示位置.以顺时针方向为导线框中电流的正方向,在下面四幅图中能够表示导线框中电流一位移(I-x)关系的是( )
如图所示,等腰三角形内以底边中垂线为界,两边分布有垂直纸面、磁感应强度大小相同且方向相反的匀强磁场,三角形高为L,长为2L,底边在x轴上.一边长为L的正方形导线框在纸面内沿x轴正方向匀速穿过匀强磁场区域,在t=0时刻恰好位于图中所示位置.以顺时针方向为导线框中电流的正方向,在下面四幅图中能够表示导线框中电流一位移(I-x)关系的是( )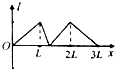


 如图所示.两个相同的小球A、B用长均为0.8m的细绳悬于小车顶部,随小车一起向右匀速运动,速度为4m/s,两球与小车前后壁接触,若某时刻小车突然停止运动,则此时悬线的拉力之比为FA:FB为( )(重力加速度g取10m/s2)
如图所示.两个相同的小球A、B用长均为0.8m的细绳悬于小车顶部,随小车一起向右匀速运动,速度为4m/s,两球与小车前后壁接触,若某时刻小车突然停止运动,则此时悬线的拉力之比为FA:FB为( )(重力加速度g取10m/s2)