题目内容
1. 如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个裝置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m的均匀导体杆ab垂直于导轨放置,且与两导轨保持良好接触,ab杆长与导轨间距相同,杆与导轨之间的动摩擦因数为μ.当杆ab在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中始终与导轨保持垂直).设杆的电阻为r,导轨电阻不计,重力加速度为g.则在此过程中( )
如图所示,固定在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个裝置处在竖直向上磁感应强度大小为B的匀强磁场中.一质量为m的均匀导体杆ab垂直于导轨放置,且与两导轨保持良好接触,ab杆长与导轨间距相同,杆与导轨之间的动摩擦因数为μ.当杆ab在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离L时,速度恰好达到最大(运动过程中始终与导轨保持垂直).设杆的电阻为r,导轨电阻不计,重力加速度为g.则在此过程中( )| A. | 杆的速度最大值为$\frac{F(R+r)}{{B}^{2}{d}^{2}}$ | |
| B. | 流过电阻R的电荷量为$\frac{BdL}{(R+r)}$ | |
| C. | 恒力F做的功大于回路中产生的电热与杆动能的变化量之和 | |
| D. | 恒力F做的功等于回路中产生的电热与杆动能的变化量之和 |
分析 当杆子所受的合力为零时速度最大,根据平衡结合闭合电路欧姆定律以及切割产生的感应电动势公式求出最大速度.根据法拉第电磁感应定律求出平均感应电动势,从而得出平均感应电流,根据q=It求出通过电阻的电量.根据动能定理判断恒力、摩擦力、安培力做功与动能的关系.
解答 解:A、当杆的速度达到最大时做匀速运动,杆受力平衡,则F-μmg-F安=0,F安=$\frac{{B}^{2}{d}^{2}{v}_{m}}{R+r}$,所以最大速度 vm=$\frac{(F-μmg)(R+r)}{{{B}^{2}d}^{2}}$.故A错误.
B、流过电阻R的电荷量为q=$\overline{I}$△t=$\frac{\overline{E}}{R+r}$△t=$\frac{△Φ}{R+r}$=$\frac{BdL}{(R+r)}$,故B正确;
CD、根据动能定理,恒力F、安培力、摩擦力做功的代数和等于杆动能的变化量,由于摩擦力做负功,所以恒力F、安培力做功的代数和大于杆动能的变化量.故C正确、D错误.
故选:BC
点评 本题综合运用了法拉第电磁感应定律以及切割产生的感应电动势的大小公式E=BLv,知道两公式的区别.要掌握安培力与感应电量的经验公式,并能灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.两个质量不同的物体,以相同的动能从地面竖直向上抛出(不计空气阻力),选地面为零势能面,当两物体上升到同一高度是,它们( )
| A. | 具有的重力势能相等 | B. | 具有的动能相等 | ||
| C. | 具有的机械能相等 | D. | 具有的机械能不相等 |
 在如图甲所示的光电计时器中,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.
在如图甲所示的光电计时器中,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间. 如图所示,质量为m=2kg的小物块从倾角θ=37°的光滑斜面上的A点由静止
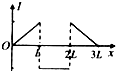
如图所示,质量为m=2kg的小物块从倾角θ=37°的光滑斜面上的A点由静止 如图所示,等腰三角形内以底边中垂线为界,两边分布有垂直纸面、磁感应强度大小相同且方向相反的匀强磁场,三角形高为L,长为2L,底边在x轴上.一边长为L的正方形导线框在纸面内沿x轴正方向匀速穿过匀强磁场区域,在t=0时刻恰好位于图中所示位置.以顺时针方向为导线框中电流的正方向,在下面四幅图中能够表示导线框中电流一位移(I-x)关系的是( )
如图所示,等腰三角形内以底边中垂线为界,两边分布有垂直纸面、磁感应强度大小相同且方向相反的匀强磁场,三角形高为L,长为2L,底边在x轴上.一边长为L的正方形导线框在纸面内沿x轴正方向匀速穿过匀强磁场区域,在t=0时刻恰好位于图中所示位置.以顺时针方向为导线框中电流的正方向,在下面四幅图中能够表示导线框中电流一位移(I-x)关系的是( )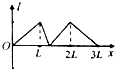


 如图所示,木板2、3为长度均为L,质置分别为m、2m,二者均放置在光滑的水平桌面上,质量为m的木块1(可视为质点)放置在木板2的最右端,木板3沿光滑水平桌面运动并与木板2发生磁撞后粘合在一起,如果要求碰后木块1停留在木板3的正中央,已知木块与木板之间的动摩擦因数为μ.
如图所示,木板2、3为长度均为L,质置分别为m、2m,二者均放置在光滑的水平桌面上,质量为m的木块1(可视为质点)放置在木板2的最右端,木板3沿光滑水平桌面运动并与木板2发生磁撞后粘合在一起,如果要求碰后木块1停留在木板3的正中央,已知木块与木板之间的动摩擦因数为μ. 如图所示.两个相同的小球A、B用长均为0.8m的细绳悬于小车顶部,随小车一起向右匀速运动,速度为4m/s,两球与小车前后壁接触,若某时刻小车突然停止运动,则此时悬线的拉力之比为FA:FB为( )(重力加速度g取10m/s2)
如图所示.两个相同的小球A、B用长均为0.8m的细绳悬于小车顶部,随小车一起向右匀速运动,速度为4m/s,两球与小车前后壁接触,若某时刻小车突然停止运动,则此时悬线的拉力之比为FA:FB为( )(重力加速度g取10m/s2) 如图所示,两光滑金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=1T、方向竖直向下的有界匀强磁场中,电阻R=1Ω,桌面高H=0.8m,金属杆ab质量m=0.2kg、接入电路部分的电阻r=1Ω,从导轨上距桌面h=0.45m高处由静止释放,落地点距桌面左边缘的水平距离s=0.8m,g=10m/s2.求:
如图所示,两光滑金属导轨,间距d=0.2m,在桌面上的部分是水平的,处在磁感应强度B=1T、方向竖直向下的有界匀强磁场中,电阻R=1Ω,桌面高H=0.8m,金属杆ab质量m=0.2kg、接入电路部分的电阻r=1Ω,从导轨上距桌面h=0.45m高处由静止释放,落地点距桌面左边缘的水平距离s=0.8m,g=10m/s2.求: