题目内容
 如图所示,长为L的轻绳一端系于固定点O,另一端系一质量为m的小球,将小球从O点正下方
如图所示,长为L的轻绳一端系于固定点O,另一端系一质量为m的小球,将小球从O点正下方| L | 4 |
(1)小球水平抛出的初速度v0;
(2)在绳被拉紧的瞬间,支点O受到的冲量.(忽略绳被拉紧的瞬间小球的重力冲量)
分析:(1)小球做平抛运动,根据竖直高度求出运动的时间,根据水平位移和时间求出小球的初速度.
(2)根据平抛运动的规律求出小球在绳子绷紧前的速度,根据动量定理求出在绳被拉紧的瞬间,支点O受到的冲量.
(2)根据平抛运动的规律求出小球在绳子绷紧前的速度,根据动量定理求出在绳被拉紧的瞬间,支点O受到的冲量.
解答:解:(1)小球被抛出后到绳拉紧前做平抛运动,绳拉紧时,小球下落高度为
h=Lcos60°-
=
水平位移x=Lsin60°=
平抛运动时间t=
=
.
则小球抛出速度v0=
=
(2)绳拉紧前瞬间,小球竖直分速度 vy=gt=
.
此时小球速度与竖直方向夹角为tanα=
=
解得 α=60°
则小球速度恰沿绳方向向外,绳拉紧时,使小球速度减为0,绳对小球的冲量
I=0-mv=-m
=-m
.
则绳对支点的冲量大小为m
,方向沿绳向外.
答:(1)小球水平抛出的初速度为
.
(2)在绳被拉紧的瞬间,支点O受到的冲量为大小为m
,方向沿绳向外.
h=Lcos60°-
| L |
| 4 |
| L |
| 4 |
水平位移x=Lsin60°=
| ||
| 2 |
平抛运动时间t=
|
|
则小球抛出速度v0=
| Lsin60° |
| t |
| ||
| 2 |
(2)绳拉紧前瞬间,小球竖直分速度 vy=gt=
|
此时小球速度与竖直方向夹角为tanα=
| v0 |
| vy |
| 3 |
解得 α=60°
则小球速度恰沿绳方向向外,绳拉紧时,使小球速度减为0,绳对小球的冲量
I=0-mv=-m
| v02+vy2 |
| 2gL |
则绳对支点的冲量大小为m
| 2gL |
答:(1)小球水平抛出的初速度为
| ||
| 2 |
(2)在绳被拉紧的瞬间,支点O受到的冲量为大小为m
| 2gL |
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道在绳被拉紧的瞬间绳子拉力远大于重力,重力的冲量可以忽略,通过动量定理求出O受到的冲量.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
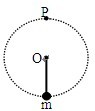 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点,且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点,且在P点受到轻杆向上的支持力 |
 (2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2
(2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2 如图所示,长为L的轻杆一端固定一个小球,另一端固定在光滑水平轴上,使小球在竖直平面内做圆周运动,设小球在过最高点A点的速度v,下列叙述中正确的是( )
如图所示,长为L的轻杆一端固定一个小球,另一端固定在光滑水平轴上,使小球在竖直平面内做圆周运动,设小球在过最高点A点的速度v,下列叙述中正确的是( ) 如图所示,长为L的轻绳一端固定于O点,另一端系一个小球.现使小球在竖直平面内做圆周运动,P是圆周轨道最高点,Q是轨道最低点.已知重力加速度为g.若小球刚好能够通过最高点P,则以下判断正确的是( )
如图所示,长为L的轻绳一端固定于O点,另一端系一个小球.现使小球在竖直平面内做圆周运动,P是圆周轨道最高点,Q是轨道最低点.已知重力加速度为g.若小球刚好能够通过最高点P,则以下判断正确的是( ) 如图所示,长为L的轻杆两端各连一个质量均为m的小球(半径可以忽略不计),以它们的中点为轴,在竖直平面内做匀速圆周运动,转动周期为T=2π
如图所示,长为L的轻杆两端各连一个质量均为m的小球(半径可以忽略不计),以它们的中点为轴,在竖直平面内做匀速圆周运动,转动周期为T=2π