Question

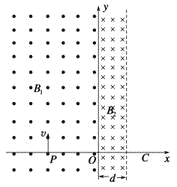
【题目】某研究学习小组设计如图游戏装置。整条联通的轨道竖直圆轨道与其两侧水平轨道组成，且圆轨道底部与两侧水平轨道平滑连接水平轨道FG右端固定一块竖直挡板N，挡板N的左侧区域AA'与BB'间有一匀强电场，场强方向水平向右。在水平轨道的P点静止释放一质量m=0.02kg，电荷量为q=2×10-3C的带电小球（可视作点电荷），若小球与N挡板碰撞，电荷量减小为碰前的k倍（k<1，碰撞前后机械能不变。已知整条轨道均是绝缘光滑的，圆轨道半径为R=0.3m，AA'与BB'间的电势差U=600V，间距为d=0.4m，P点距离BB'为d，不计空气阻力，设BB'处的电势为零，则：

（1）小球在P点的电势能多大；

（2）k满足什么条件时，小球与N挡板共碰撞2次，且不脱离圆轨道；

（3）若k=，小球在电场中运动的总路程为多少?

Answer 1

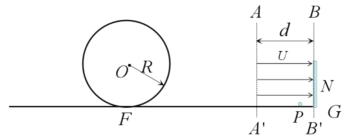
【答案】（1）0.3J;（2）;（3）1.1m

【解析】

(1)PN间场强

E==1500V/m

电势差

U1=Ed1=150V

有

qU1=EP－0

求得

EP=0.3J

(2)小球第一次与挡板N碰撞后不能超过圆心等高处，即

qEd1+kq(-U)≤mgR

求

小球第二次通过圆最高点

求得

有

qEd1+k2q(－U)≥mg2R+

求得

因此取

(3)小球第一次与挡板碰撞后出电场的条件是

qEd1+kq(－U)≥0

即

k≤

若k=，小球第一次与挡板碰撞后没出电场，因此

qEd1－kqEx=0

得

x=0.3m

第二次碰撞后却可以离开电场并通过圆轨道最高点，因此在电场中总路程为

s=d1+2x+d=1.1m