题目内容
2. 如图所示,质量为M的小车在光滑的水平面上以v0向右匀速运动,一个质量为m的小球从高h处自由下落,与小车碰撞后,又反弹上升的最大高度仍为h.设M》m,发生碰撞时弹力N>mg,球与车之间的动摩擦因数为μ.则小球弹起的水平速度可能是( )
如图所示,质量为M的小车在光滑的水平面上以v0向右匀速运动,一个质量为m的小球从高h处自由下落,与小车碰撞后,又反弹上升的最大高度仍为h.设M》m,发生碰撞时弹力N>mg,球与车之间的动摩擦因数为μ.则小球弹起的水平速度可能是( )| A. | v0 | B. | 0 | C. | 2μ$\sqrt{2gh}$ | D. | -v0 |
分析 小球的水平速度是由于小车对它的摩擦力作用引起的,若小球在离开小车之前水平方向上就已经达到了v0,则摩擦力消失,小球在水平方向上的速度不再加速;反之,小球在离开小车之前在水平方向上就是一直被加速的.然后使用动量定理分别沿水平方向和竖直方向分析,即可得出结论.
解答 解:该题需要分以下两种情况进行分析:
①小球离开小车之前已经与小车达到共同速度v,则水平方向上动量守恒,有:
Mv0=(M+m)v
由于M?m
所以:v=v0;
②若小球离开小车之前始终未与小车达到共同速度,则对小球应用动量定理,水平方向上有:
Fμt=mv′
小球反弹后上升的高度为h,则反弹的速度v与落在小车上时的速度大小相等,以向上为正方向,竖直方向上有:
FNt=mv-m(-v)=2m$\sqrt{2gh}$,
又 Fμ=μFN
解得:v′=2μ$\sqrt{2gh}$;
故选:AC.
点评 该题中由于碰撞的时间不知,所以小球在水平方向的运动有两种情况,这是解决该题的关键,也是容易被忽略的地方.

练习册系列答案
相关题目
13.对于一定质量的理想气体,从微观的角度解释,下列说法中正确的是( )
| A. | 在温度不变时,气体的体积增大,分子每次与器壁碰撞时冲量减小,气体压强减小 | |
| B. | 在体积不变时,气体的温度升高,平均每个气体分子对器壁产生的冲量增大,压强增大 | |
| C. | 在体积不变时,气体的温度升高,平均每个气体分子对器壁产生的冲量减小,压强增大 | |
| D. | 在压强不变时,气体温度升高,平均每个气体分子对器壁产生的冲量减小,减小单位面积上碰撞次数,使体积增大 |
7.关于波速公式v=λf,下面哪几句话是正确的( )
| A. | 适用于一切波 | |
| B. | 对同一机械波来说,通过不同的介质时,频率f不变 | |
| C. | 一列绳波的振动频率f变大,λ要减小 | |
| D. | 声音由空气传入水中,f 不变,λ减小 |
11.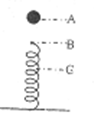 如图所示,小球自A点由静止开始自由下落,到B点时与竖直放置的轻弹簧接触,到C点时弹簧被压至最短,若不计空气阻力,在小球由A-B-C的运动过程中( )
如图所示,小球自A点由静止开始自由下落,到B点时与竖直放置的轻弹簧接触,到C点时弹簧被压至最短,若不计空气阻力,在小球由A-B-C的运动过程中( )
 如图所示,小球自A点由静止开始自由下落,到B点时与竖直放置的轻弹簧接触,到C点时弹簧被压至最短,若不计空气阻力,在小球由A-B-C的运动过程中( )
如图所示,小球自A点由静止开始自由下落,到B点时与竖直放置的轻弹簧接触,到C点时弹簧被压至最短,若不计空气阻力,在小球由A-B-C的运动过程中( )| A. | 小球的动能先增加后减小 | |
| B. | 小球刚接触弹簧时动能最大 | |
| C. | 小球动能最大时弹簧的弹性势能为零 | |
| D. | 小球动能减为零时,重力势能最大 |
12.如图所示,一辆向右行驶的汽车将一重物A匀速提起,在此过程中,说法正确的是( )
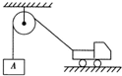

| A. | 汽车向右减速行驶,且车所受地面的支持力增大 | |
| B. | 汽车向右减速行驶,且所受地面摩擦力不变 | |
| C. | 汽车向右匀速行驶,且所受地面摩擦力不变 | |
| D. | 汽车向右匀速行驶,且车所受牵引力减小 |
