题目内容
14.某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为99.00cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为100.0s.则:(1)他测得的重力加速度g=9.86m/s2.(计算结果取三位有效数字)
(2)他测得的g值偏大,可能原因是:ACD.
A.测摆线长时摆线拉得过紧.
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了.
C.开始计时时,秒表过迟按下.
D.实验中误将49次全振动计为50次.
(3)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l和T的数值,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率k.则重力加速度 g=$\frac{4{π}^{2}}{k}$.(用k表示)
分析 (1)单摆的摆长等于摆线的长度与摆球的半径之和;根据单摆的周期公式得出重力加速度g的数值.
(2)根据单摆的周期公式得出重力加速度g的表达式,从而判断出g值偏大的原因.
(3)由单摆周期表达式可得T2与L的关系式,得到斜率k的表达式,进而可求得g值.
解答 解:(1)摆长为:L=l+$\frac{d}{2}$=99.00cm+1.00cm=100.00cm=1.0000m;
单摆振动50次所用的时间为100.0s,则周期:T=$\frac{t}{n}=\frac{100.0}{50}=2.00$s
根据T=2π $\sqrt{\frac{L}{g}}$,得:g=$\frac{4{π}^{2}L}{{T}^{2}}$=$\frac{4×3.1{4}^{2}×1.0000}{2.0{0}^{2}}=9.86m/{s}^{2}$.
(2)根据T=2π $\sqrt{\frac{L}{g}}$,得:g=$\frac{4{π}^{2}L}{{T}^{2}}$
A、测量摆长时,线拉得过紧,则摆长的测量值偏大,由上式可知重力加速度测量值偏大,故A正确.
B、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,则对应的周期变大,周期的测量值偏大,则加速度的测量值偏小.故B错误.
C、开始计时时,秒表过迟按下,周期的测量值偏小,由上式可知重力加速度测量值偏大.故C正确.
D、实验中误将49次全振动记为50次,周期的测量值偏小,由上式可知重力加速度测量值偏大,故D正确.
故选:ACD.
(3)根据T=2π $\sqrt{\frac{L}{g}}$,得T2=$\frac{4{π}^{2}L}{g}$
故以L为横坐标、T2为纵坐标得到的图象的斜率为:k=$\frac{4{π}^{2}}{g}$
解得:g=$\frac{4{π}^{2}}{k}$
故答案为:(1)9.86;(2)ACD;(3)$\frac{4{π}^{2}}{k}$
点评 本题关键要掌握实验的原理:单摆的周期公式T=2π $\sqrt{\frac{L}{g}}$,要能根据实验原理,分析实验误差;推导出T2-L的关系图象,得到斜率的表达式,基础问题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 查德威克通过实验发现了中子的核反应方程为:${\;}_{2}^{4}$He+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | |
| B. | 放射性元素的半衰期与原子所处的物理状态或化学状态有关 | |
| C. | α射线是原子核发生衰变时放射出得氦核流,它的电离作用非常弱 | |
| D. | 卢瑟福α粒子散射实验的结果证明了原子的全部正电荷和几乎全部质量都集中在一个很小的核上 |
 如图所示,质量为M的小车在光滑的水平面上以v0向右匀速运动,一个质量为m的小球从高h处自由下落,与小车碰撞后,又反弹上升的最大高度仍为h.设M》m,发生碰撞时弹力N>mg,球与车之间的动摩擦因数为μ.则小球弹起的水平速度可能是( )
如图所示,质量为M的小车在光滑的水平面上以v0向右匀速运动,一个质量为m的小球从高h处自由下落,与小车碰撞后,又反弹上升的最大高度仍为h.设M》m,发生碰撞时弹力N>mg,球与车之间的动摩擦因数为μ.则小球弹起的水平速度可能是( )| A. | v0 | B. | 0 | C. | 2μ$\sqrt{2gh}$ | D. | -v0 |
| A. | 从微观上讲,气体的压强是大量的气体分子无规则运动不断撞击器壁产生的 | |
| B. | 只从单一热源吸热,使之完全变为有用功而不产生其他影响的机器是可以制造出来的 | |
| C. | 温度升高时,气体的压强一定增大 | |
| D. | 绝对零度不可达到 |

 为了测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0cm的遮光板,如图所示,滑块在牵引力作用下先后匀加速通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.30s,通过第二个光电门的时间为△t2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.0s.则滑块的加速度是0.067m/s2(结果保留2位有效数字)
为了测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0cm的遮光板,如图所示,滑块在牵引力作用下先后匀加速通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为△t1=0.30s,通过第二个光电门的时间为△t2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t=3.0s.则滑块的加速度是0.067m/s2(结果保留2位有效数字)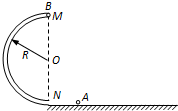 如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求
如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R.重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求