Question

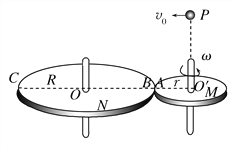
【题目】如图所示，靠在一起的M、N两转盘靠摩擦传动，两盘均绕过圆心的竖直轴转动，M盘的半径为r，N盘的半径R＝2r.A为M盘边缘上的一点，B、C为N盘直径的两个端点．当O′、A、B、C共线时，从O′的正上方P点以初速度v0沿O′O方向水平抛出一小球．小球落至圆盘C点，重力加速度为g.则下列说法正确的是(　　)

A. 若M盘转动角速度，则小球抛出时到O′的高度为

B. 若小球抛出时到O′的高度为，则M盘转动的角速度必为

C. 只要M盘转动角速度满足，小球就可能落至C点

D. 只要小球抛出时到O′的高度恰当，小球就可能落至C点

Answer 1

【答案】A

【解析】若M盘转动角速度为ω，则N转动的角速度为；根据平抛运动的规律知h=gt2，x=v0t；当t= ，n=1、2、3…，x=r+2R=5r时小球可落到C点；若t=，且x=r，n=1、2、3…，即 或者，若M盘转动角速度 ，则x=r，n=1，时间t=，h=gt2=，故A正确；根据A分析知，只要满足（n=1、2、3…）即可，故B错误；根据A分析知角速度满足（n=1、2、3…）或者（n=1、2、3…），均可落到C点，故C错误；根据以上分析要想到达C点，除了考虑高度还与初速度有关，故D错误；故选A。