题目内容
19. 如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )
如图所示,质量为m的A,B两球分别固定在长为L的轻杆的一端和中点,转至最高点A球速度v时,轻杆对A球作用力刚好为零,在最高点,若A球速度为4v时,轻杆OB对B球的作用力为( )| A. | 16mg | B. | 22mg | C. | 28mg | D. | 0 |
分析 根据牛顿第二定律求出A小球在最高点的速度,再求出速度为4V时AB段杆对A球的拉力,A、B两球角速度相等,求出B球的线速度.再根据牛顿第二定律求出OB杆子对B球的拉力大小.
解答 解:在最高点A球速度为v时,因为轻杆对A球作用力恰好为零,
这时对A球:它的重力完全提供向心力.
mg=$m\frac{{v}^{2}}{L}$得
v=$\sqrt{gL}$
在最高点A球速度为4v时,可知AB段杆对A球的作用力方向是向下的.
这时对A球:F1=mg+Fab=$m\frac{{(4v)}^{2}}{L}$,Fab是AB段杆对A球的拉力.
得 Fab=15*mg
这时对B球:受竖直向下的重力mg、OB段杆对它的竖直向下的拉力Fob、AB杆对它的竖直向上的拉力Fab.
得 Fob+mg-Fab=$m\frac{{{v}_{b}}^{2}}{\frac{L}{2}}$
B球速度是 Vb=2V (因为两球角速度相同,且B球在杆中间)
即 Fob+mg-Fab=$\frac{m(2v)^{2}}{\frac{L}{2}}$
得 Fob=22mg
即轻杆OB对B球的作用力大小是Fob=22mg
故选:B
点评 解决本题的关键搞清小球做圆周运动向心力的来源,再运用牛顿第二定律进行求解,知道AB共轴转动,角速度相等,难度不大,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.质点是一种理想化的物理模型,下面对质点的理解正确的是( )
| A. | 只有体积很小的物体才可以看作质点 | |
| B. | 只有质量很小的物体才可以看作质点 | |
| C. | 计算火星绕太阳运动的速度时,可将火星看作质点 | |
| D. | 地球的质量和体积很大,所以在任何情况下都不能将地球看作质点 |
10. 甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
 甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )| A. | 两人的线速度相同,为2m/s | |
| B. | 两人的角速度相同,为2rad/s | |
| C. | 两人的运动半径相同,都是1m | |
| D. | 两人的运动半径不同,甲为0.8m,乙为1.2m |
4.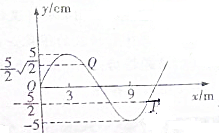 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )| A. | 质点P此时可的振动方向沿y轴负方向 | |
| B. | 质点P的振幅比质点Q的振幅小 | |
| C. | 波的频率为0.25Hz | |
| D. | 质点P,Q的平衡位置间距离为6.5m | |
| E. | 从图示时刻开始,再经$\frac{7}{12}$s,质点P,Q的位移第一次相等 |
6.在云南省某些地方到现在还要依靠滑铁索过江,若把这滑铁索过江简化成如图所示的模型,铁索的两个固定点A、B在同一水平面内,AB间的距离为L=80m,绳索的最低点离AB间的垂直距离为H=8m,若把绳索看做是圆弧,已知一质量m=52kg的人借助滑轮(滑轮质量不计)滑到最低点的速度为10m/s,那么( )


| A. | 人在整个绳索上运动可看成是匀速圆周运动 | |
| B. | 可求得绳索的圆弧半径为100m | |
| C. | 人在滑到最低点时,滑轮对绳索的压力为570N | |
| D. | 在滑到到最低点时人处于超重状态 |
 如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?
如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?
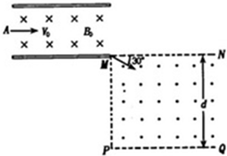 如图所示,有一对平行金属板,板间加有恒定电压;两板间有匀强磁场,磁感应强度大小为B0,方向垂直于纸面向里.金属板右下方以MN、PQ为上、下边界,MP为左边界的区域内,存在垂直纸面向我的匀强磁场,磁场宽度为d,MN与下极板等高,MP与金属板右端在同一竖直线.一电荷量为q、质量为m的正离子,以初速度v0沿平行于金属板面、垂直于板间磁场的方向从A点射入金属板间,不计离子的重力.
如图所示,有一对平行金属板,板间加有恒定电压;两板间有匀强磁场,磁感应强度大小为B0,方向垂直于纸面向里.金属板右下方以MN、PQ为上、下边界,MP为左边界的区域内,存在垂直纸面向我的匀强磁场,磁场宽度为d,MN与下极板等高,MP与金属板右端在同一竖直线.一电荷量为q、质量为m的正离子,以初速度v0沿平行于金属板面、垂直于板间磁场的方向从A点射入金属板间,不计离子的重力.