题目内容
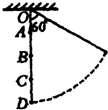
一根长为l不可伸长的轻绳，一端系一小球，另一端悬挂于O点．将小球拉起使轻绳拉直并与竖直方向成60°角，如图所示，在O点正下方有A、B、C三点，并且有hOA=hAB=hBC=hCD=
l．当在A处钉钉子时，小球由静止下摆，被钉子档住后继续摆动的最大高度为hA；当在B处钉钉子时，小球由静止下摆，被钉子档住后继续摆动的最大高度为hB；当在C钉子时，小球由静止下摆，被钉子挡住后继续摆动的最大高度hC，则小球摆动的最大高度hA、hB、hC之间的关系是（ ）
| 1 |
| 4 |
| A．hA=hB=hC | B．hA＞hB＞hC | C．hA＞hB=hC | D．hA=hB＞hC |
小球拉开60°放手，故小球升高的高度为：
h=L-Lcos60°=
L
由机械能守恒定律可知，由mgh=
mv2得：
到达最低点的速度：v=
钉子在A、B两时，小球能摆到等高的位置hA=hB；
当钉子放在C点时，小球摆到最低点后开始以C点为圆心，以
L为半径做圆周运动，若能到达最高点，最高点处有最小速度，速度不能为零；但由机械能守恒知，如果能到达最高点，速度为零；故小球无法到达最高点；所以上升不到原下落点高度，故hA=hB＞hC
故选D．
h=L-Lcos60°=
| 1 |
| 2 |
由机械能守恒定律可知，由mgh=
| 1 |
| 2 |
到达最低点的速度：v=
| gL |
当钉子放在C点时，小球摆到最低点后开始以C点为圆心，以
| 1 |
| 4 |
故选D．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图所示，一根长为l不可伸长的细丝线一端固定于O点，另一端系住一个质量为m的带电小球．将此装置放在水平向右的匀强电场E中，待小球稳定后，细丝线跟竖直方向夹角为α，求：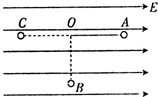
如图所示．在竖直平面内一个带正电的小球质量为m，所带的电荷量为q，用一根长为L不可伸长的绝缘细线系在一匀强电场中的O点．匀强电场方向水平向右，分布的区域足够大．现将带正电小球从O点右方由水平位置A点无初速度释放，小球到达最低点B时速度恰好为零．
（2008?天津模拟）一根长为l不可伸长的轻绳，一端系一小球，另一端悬挂于O点．将小球拉起使轻绳拉直并与竖直方向成60°角，如图所示，在O点正下方有A、B、C三点，并且有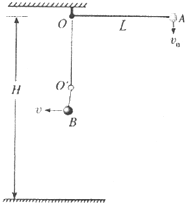
在离地面高H=2L的O点，固定一根长为L不可伸长的细轻绳，绳端系一质量为m、带电量为+q的小球，整个空间存在竖直向下的匀强电场（图中未画出），电场强度E=