题目内容
 如图所示,一根长为l不可伸长的细丝线一端固定于O点,另一端系住一个质量为m的带电小球.将此装置放在水平向右的匀强电场E中,待小球稳定后,细丝线跟竖直方向夹角为α,求:
如图所示,一根长为l不可伸长的细丝线一端固定于O点,另一端系住一个质量为m的带电小球.将此装置放在水平向右的匀强电场E中,待小球稳定后,细丝线跟竖直方向夹角为α,求:(1)小球带什么电?电量是多少?
(2)保持小球带电量不变,用外力将小球缓慢拉到竖直方向的最低点,外力对小球做多少功?
分析:(1)小球稳定后,细丝线跟竖直方向夹角为α,对小球进行受力分析即可判断小球的电性,根据力的合成与分解即可求得电量;
(2)用外力将小球缓慢拉到竖直方向的最低点的过程中,小球始终处于平衡状态,动能不变,根据动能定理即可解题.
(2)用外力将小球缓慢拉到竖直方向的最低点的过程中,小球始终处于平衡状态,动能不变,根据动能定理即可解题.
解答:解: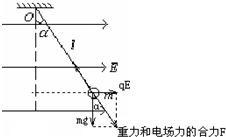 (1)对小球进行受力分析:由于小球所受电场力水平向右,E的方向水平向右,所以小球带正电.小球受力如图所示,
(1)对小球进行受力分析:由于小球所受电场力水平向右,E的方向水平向右,所以小球带正电.小球受力如图所示,
qE=mgtanα①
即q=
(2)将小球缓慢拉到竖直方向的最低点的过程中,小球动能变化量为零,设外力小球做功为W,由动能定理可知:
W+mgl(1-cosα)-qElsinα=0②
由①②式得:W=mgl(
-1)
答:(1)小球带正电,电量为
;
(2)保持小球带电量不变,用外力将小球缓慢拉到竖直方向的最低点,外力对小球做的功为mgl(
-1).
 (1)对小球进行受力分析:由于小球所受电场力水平向右,E的方向水平向右,所以小球带正电.小球受力如图所示,
(1)对小球进行受力分析:由于小球所受电场力水平向右,E的方向水平向右,所以小球带正电.小球受力如图所示,qE=mgtanα①
即q=
| mgtanα |
| E |
(2)将小球缓慢拉到竖直方向的最低点的过程中,小球动能变化量为零,设外力小球做功为W,由动能定理可知:
W+mgl(1-cosα)-qElsinα=0②
由①②式得:W=mgl(
| 1 |
| cosα |
答:(1)小球带正电,电量为
| mgtanα |
| E |
(2)保持小球带电量不变,用外力将小球缓慢拉到竖直方向的最低点,外力对小球做的功为mgl(
| 1 |
| cosα |
点评:本题主要考查了同学们受力分析的能力以及动能定理的直接应用,难度不大,属于基础题.

练习册系列答案
相关题目
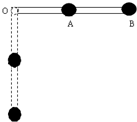 如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )
如图所示,一根长为L,质量不计的硬杆,在中点及右端各固定一个质量为m的小球,杆可带动小球在竖直平面内绕O点转动.若开始时杆处于水平位置,由静止开始释放,当杆下落到竖直位置时,下列说法中正确的是( )A、B球的速率为
| ||||
B、B球的机械能减少了
| ||||
C、A球的机械能减少了
| ||||
| D、每个小球的机械能都不变 |
 如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )
如图所示,一根长为L的细杆的一端固定一质量为m的小球,整个系统绕杆的另一端在竖直面内做圆周运动,且小球恰能过最高点.已知重力加速度为g,细杆的质量不计.下列说法正确的是( )A、小球过最低点时的速度大小为
| ||
B、小球过最高点时的速度大小为
| ||
| C、小球过最低点时受到杆的拉力大小为5mg | ||
| D、小球过最高点时受到杆的支持力为零 |
 如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端
如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端 如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( )
如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( ) 如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为
如图所示,一根长为l的轻杆的一端与一个质量为m为小球相连,并可绕过另一端O点的水平轴在竖直面内自由转动,图中的a、b分别表示小球运动轨迹的最低点和最高点,已知杆能提供的最大支持力为