题目内容
在一根长为L不可伸长的轻质线一端系一质量为m的小球,线的另一端系于O点.把球拉到水平后静止释放,问:小球运动到什么位置具有最大的竖直分速度?
分析:小球在竖直方向先做加速运动后做减速运动,当小球竖直方向受到的合力等于零的瞬间,其速度最大.此时由重力沿绳子方向的分力和拉力的合力提供向心力,根据牛顿第二定律列出绳子拉力与速度的关系.再由机械能守恒定律,求出小球最大的竖直分速度.
解答:解:小球受力如图所示.
 在下落过程中绳子拉力T逐渐增大,根据力的独立作用原理,在竖直方向上有
在下落过程中绳子拉力T逐渐增大,根据力的独立作用原理,在竖直方向上有
mg-Tcosα=may
竖直方向的分运动的加速度逐渐减小,速度逐渐增大,当ay=0,即mg=Tcosα时,vy达到最大值,此后Tcosα大于mg,ay竖直向上,物体的竖直分速度将减小.当小球竖直分速度vy最大时,有
mg=Tcosα…①
T-mgcosα=m
…②
根据机械能守恒定律得
mgLcosα=
mv2…③
取立①②③式得:cosα=
,即:α=arccos
.
最大竖直分速度为:vy=vsinα=
?sinα=
gL.
答:小球运动到绳子与竖直方向的夹角为α=arccos
时具有最大的竖直分速度.
 在下落过程中绳子拉力T逐渐增大,根据力的独立作用原理,在竖直方向上有
在下落过程中绳子拉力T逐渐增大,根据力的独立作用原理,在竖直方向上有mg-Tcosα=may
竖直方向的分运动的加速度逐渐减小,速度逐渐增大,当ay=0,即mg=Tcosα时,vy达到最大值,此后Tcosα大于mg,ay竖直向上,物体的竖直分速度将减小.当小球竖直分速度vy最大时,有
mg=Tcosα…①
T-mgcosα=m
| v2 |
| L |
根据机械能守恒定律得
mgLcosα=
| 1 |
| 2 |
取立①②③式得:cosα=
| ||
| 3 |
| ||
| 3 |
最大竖直分速度为:vy=vsinα=
| 2gLcosα |
|
答:小球运动到绳子与竖直方向的夹角为α=arccos
| ||
| 3 |
点评:本题是向心力知识和机械能守恒定律的综合,可以用极限法分析小球在竖直方向的运动情况.

练习册系列答案
相关题目
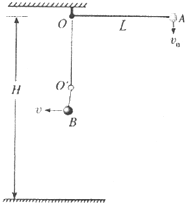 在离地面高H=2L的O点,固定一根长为L不可伸长的细轻绳,绳端系一质量为m、带电量为+q的小球,整个空间存在竖直向下的匀强电场(图中未画出),电场强度E=
在离地面高H=2L的O点,固定一根长为L不可伸长的细轻绳,绳端系一质量为m、带电量为+q的小球,整个空间存在竖直向下的匀强电场(图中未画出),电场强度E=