Question

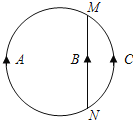
【题目】如图所示，半径分别为R和r（R＞r）的甲、乙两光滑圆轨道安置在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，在水平轨道CD上一轻弹簧被a、b两小球夹住，同时释放两小球，a、b球恰好能通过各自的圆轨道的最高点。则两小球的质量之比为

A. B. C. D.

Answer 1

【答案】B

【解析】

ab球恰好能通过各自的圆轨道的最高点，均由重力提供向心力，可根据牛顿第二定律求出两球通过最高点时的速度；脱离弹簧到圆轨道最高点过程中，a球的机械能守恒，根据a球机械能守恒，求出弹簧弹开两小球时a球的速度；要弹簧释放过程中，两球及弹簧组成的系统动量守恒，即可由动量守恒定律求出ma：mb。

ab球恰好能通过各自的圆轨道的最高点，则有均由重力提供向心力，即有

对于a球：得，

对于b球：得，

a球脱离弹簧到圆轨道最高点过程机械能守恒：

所以a球脱离弹簧时速度：

b球脱离弹簧到圆轨道最高点过程机械能守恒：

所以b球脱离弹簧时速度：

弹簧释放过程中，由动量守恒定律得：mava=mbvb

得，，故B正确，ACD错误。

故选B。