题目内容
如图所示为固定在桌面上的“C”形木块,abcd为光滑圆轨道的一部分,a为轨道的最高点,de面水平.将质量为m的小球在d点正上方h高处释放,小球自由下落到d处后沿切线进入圆形轨道运动,( )
| A.在h一定的条件下,释放后小球能否到a点,与小球质量有关 |
| B.改变h的大小,就可使小球在通过a点后落回轨道之内,或者落在de面上 |
| C.要使小球通过a点的条件是在a点的速度v>0 |
| D.无论怎样改变h的大小,都不可能使小球在通过a点后又落回轨道内 |
D
解析试题分析:小球恰能通过a点的条件是小球的重力提供向心力,根据牛顿第二定律: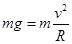 ,解得:
,解得: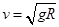 ,要使小球能到a点,要使小球通过a点的条件是在a点速度大于等于
,要使小球能到a点,要使小球通过a点的条件是在a点速度大于等于 ,根据动能定理可以求出h的最小值,与小球质量有关,故AC错误;小球恰好离开a点时做平抛运动,用平抛运动的规律,
,根据动能定理可以求出h的最小值,与小球质量有关,故AC错误;小球恰好离开a点时做平抛运动,用平抛运动的规律,
水平方向的匀速直线运动: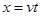 ,竖直方向的自由落体运动:
,竖直方向的自由落体运动: 解得:
解得: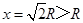 ,所以小球在通过a点后不可能落回轨道之内,故B错误,D正确,
,所以小球在通过a点后不可能落回轨道之内,故B错误,D正确,
考点:考查了机械能守恒定律;自由落体运动。

某实验小组采用如图所示的装置研究“小车运动变化规律”。打点计时器工作频率为50Hz。
实验的部分步骤如下: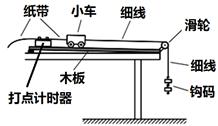
a.将木板的左端垫起,以平衡小车的摩擦力;
b.在小车中放入砝码,纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
c.将小车停在打点计时器附近,接通电源,释放小车,小车拖动纸带,打点计时器在纸带上打下一系列的点,断开电源;
d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作。
(1)设钩码质量为m1、砝码和小车总质量为m2,重力加速度为g,则小车的加速度为:a=(用题中所给字母表示);
(2)下图是某次实验中得到的一条纸带,在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v。请将C点对应的测量xC值和计算速度vC值填在下表中的相应位置。
| 计数点 | x/cm | s/cm | v/(m·s-1) |
| O | 1.00 | | 0.30 |
| A | 2.34 | 1.34 | 0.38 |
| B | 4.04 | 3.04 | 0.46 |
| C | | 5.00 | |
| D | 8.33 | 7.33 | 0.61 |
| E | 10.90 | 9.90 | 0.70 |
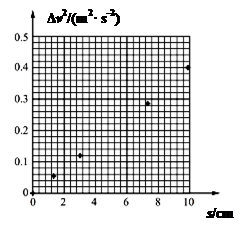
(3)实验小组通过绘制Δv2-s图线来分析运动规律(其中Δv2=v2-v02,v是各计数点对应时刻小车的瞬时速度,v0是O点对应时刻小车的瞬时速度)。他们根据实验数据在图中标出了O、A、B、D、E对应的坐标点,请你在该图中标出计数点C对应的坐标点,并画出Δv2-s图线。
(4)实验小组绘制的Δv2-s图线的斜率k =(用题中所给字母表示),若发现该斜率大于理论值,其原因可能是。
如图所示,用一把直尺可以测量神经系统的反应速度。现有甲、乙两同学,甲同学用手指拿着一把长50cm的直尺,乙同学把手放在零刻度线位置做抓尺的准备,当甲同学松开直尺,乙同学见到直尺下落时,立即用手抓住直尺,记录抓住处的数据,重复以上步骤多次。现有乙同学测定神经系统的反应速度得到以下数据(单位:cm),则下列说法正确的是( )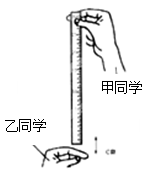
| 第一次 | 第二次 | 第三次 |
| 20 | 45 | 30 |
A.第一次测量的反应时间最长
B.第一次测量的反应时间为2s
C.第二次抓住之前的瞬间,直尺的速度约为4m/s
D.若某同学的反应时间为0.4s,则该直尺将无法测量该同学的反应时间
为了求出楼房的高度,让一石子从楼顶自由下落,若空气阻力作用不计,仅测出下列哪个物理量的值不能计算出楼房高度的是( )
| A.石子下落的时间 |
| B.石子落地时的速度 |
| C.石子下落头1s内的位移 |
| D.石子通过最后1m的时间 |
如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等,有三个完全相同的小球a、b、c.开始均静止于斜面同一高度处,其中b小球在两斜面之间.若同时释放a、b、c小球到达该水平面的时间分别为t1、t2、t3.若同时沿水平方向抛出,初速度方向如图所示,到达该水平面的时间分别为t1′、t2′、t3′.下列关于时间的关系正确的是( )
| A.t1>t3>t2 | B.t1=t1′、t2=t2′、t3=t3′ |
| C.t1′>t3′>t2′ | D.t1<t1′、t2<t2′、t3<t3′ |
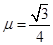 ,且
,且 。第一次,m1悬空(未与斜面体接触),m2放在斜面上,m2自斜面底端由静止开始运动至斜面顶端所用的时间为
。第一次,m1悬空(未与斜面体接触),m2放在斜面上,m2自斜面底端由静止开始运动至斜面顶端所用的时间为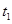 ;第二次,将m1和m2位置互换,使 m2 悬空,m1放在斜面上,则 m1 自斜面底端由静止开始运动至斜面顶端所需的时间为
;第二次,将m1和m2位置互换,使 m2 悬空,m1放在斜面上,则 m1 自斜面底端由静止开始运动至斜面顶端所需的时间为 。求
。求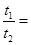 ?
?


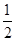 h B
h B 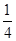 h C
h C  h D
h D  h
h