题目内容
9.某同学要测量一个由均匀新材料制成的圆柱体的电阻率ρ,步骤如下:
(1)用20分度的游标卡尺测量其长度如图甲所示,可知其长度为50.20mm;
(2)用螺旋测微器测量其直径如图乙所示,可知其直径为4.699mm;
(3)用多用电表的电阻“×10”档,按正确的操作步骤粗测此圆柱体的电阻,表盘的示数如图丙所示,则该电阻的阻值约为220Ω;
(4)为更精确地测量其电阻,现有的器材及其代号和规格如下:
待测圆柱体电阻R
电流表A1(量程0~3mA,内阻约50Ω)电流表A2(量程0~15mA,内阻约30Ω)
电压表V1(量程0~3V,内阻约10kΩ)电流表V2(量程0~15V,内阻约25kΩ)
滑动变阻器R1(阻值范围0~15Ω)滑动变阻器R2(阻值范围0~2kΩ)
直流电源(电动势4V,内阻不计) 开关S,导线若干
为使实验误差较小,要求测得多组数据进行分析,电流表应选用A2,电压表应选用V1,请在图丁方框中画出测量用的正确图,并标明所用器材的代号.
分析 (1)游标卡尺读数时应分成整数部分和小数部分两部分来读,注意分度大小;
(2)螺旋测微器读数时应分成整数部分和小数部分两部分来读,注意半毫米刻度线是否露出;
(3)欧姆表指针示数与挡位的乘积是欧姆表示数;
(4)首先根据电源电动势大小选择出电压表的量程,再通过求出通过待测电阻的最大电流来选择电流表量程,根据电流表内外接法的选择方法判定应采用内接法;根据要求多测几组数据可知变阻器应采用分压式接法,即电路应是分压外接电路.
解答 解;(1)游标卡尺的读数为:L=50mm+4×0.05mm=50.20mm;
(2)螺旋测微器的读数为:D=4.5mm+19.9×0.01mm=4.699(4.700±0.001);
(3)欧姆表的读数为:R=22×10Ω=220Ω;
(4)根据电源的电动势为4V可知电压表应选择V1;
由于通过待测电阻的最大电流为Imax=$\frac{E}{{R}_{x}}$=$\frac{4}{300}$A=13mA,所以电流表应选择A1;
由于待测电阻满足$\frac{{R}_{V}}{{R}_{x}}$>$\frac{{R}_{x}}{{R}_{A}}$,所以电流表应用外接法;
由于实验要求能测多组数据,所以变阻器应采用分压式接法,电路图如图所示:
故答案为:(1)50.20;(2)4.699;(3)220;(4)A2,V1.电路图如上图所示.
点评 应明确:①游标卡尺和螺旋测微器读数时应分成整数部分和小数部分两部分来读;②根据电源电动势大小来选择电压表的量程,根据通过待测电阻的最大电流来选择电流表的量程,若实验要求多测几组数据或要求电压从零调或不正确的全电阻远小于待测电阻时,变阻器应采用分压式接法;③当待测电阻满足$\frac{{R}_{V}}{{R}_{x}}$>$\frac{{R}_{x}}{{R}_{A}}$时,电流表应用外接法,满足$\frac{{R}_{V}}{{R}_{x}}$<$\frac{{R}_{x}}{{R}_{A}}$时电流表应用内接法.

 名校课堂系列答案
名校课堂系列答案| A. | 物体的速度一定增加的越来越慢 | B. | 物体运动的速度一定减小 | ||
| C. | 物体的速度变化量一定减少 | D. | 物体运动的路程一定增大 |
| A. | nT | B. | $\frac{T}{n}$ | C. | T$\sqrt{n}$ | D. | $\frac{T}{\sqrt{n}}$ |
 某同学欲准确测定一个量程为3V,内阻约为2kΩ的电压表的内阻.所备器材有:
某同学欲准确测定一个量程为3V,内阻约为2kΩ的电压表的内阻.所备器材有:A.待测电压表:量程3V,内阻约为2kΩ
B.电流表:量程10mA,内阻约为50Ω
C.定值电阻:R1=400Ω
D.滑动变阻器R2:最大阻值20Ω
E.直流电源:电动势E-6V,内阻可不计
F.开关,导线若干
为保证测量结果的准确性,实验要求两表指针偏转的最大刻度都要超过总量程的$\frac{1}{2}$.
(1)在图1空格中补全实验电路;
(2)改变滑动变阻器的阻值,读取实验数据填入如下表格,依据表格中的U,I数据在图2坐标纸上画出U-I图线;
| 电压U/V | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
| 电流I/mA | 0 | 1.49 | 3.00 | 4.52 | 6.00 | 6.98 | 8.96 |
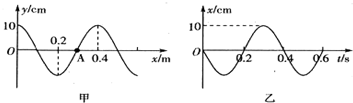
| A. | 该列波沿x轴负方向传播 | |
| B. | 该列波的波速大小为1m/s | |
| C. | 若此波遇到另一列简谐横渡并发生稳定干涉现象,则所遇到的波的频率为0.4Hz | |
| D. | 若该波遇到一障碍物发生了明显的衍射现象,则该障碍物的尺寸和40cm差不多或更小 | |
| E. | 从该时刻起,再经过0.4s的时间,质点A通过的路程为40cm |
| A. | $\frac{v_1}{v_2}=\frac{r}{R};\frac{a_1}{a_2}=\frac{r}{R}$ | B. | $\frac{v_1}{v_2}=\sqrt{\frac{r}{R}};\frac{a_1}{a_2}=\frac{r^2}{R^2}$ | ||
| C. | $\frac{v_1}{v_2}=\sqrt{\frac{R}{r}};\frac{a_1}{a_2}=\frac{R^2}{r^2}$ | D. | $\frac{v_1}{v_2}=\frac{R}{r};\frac{a_1}{a_2}=\frac{R}{r}$ |
 三个平行金属板a、b、c,ab相距d1,bc相距d2,d2=d1,三个金属板上分别有三个小孔A、B和C,其连线跟板面垂直,三个金属板接到电动势为ε1和ε2的两个电源上,如图所示,ε1<ε2,在A孔的右侧放一个带负电的质点(不计重力),由静止开始释放后,质点将向右运动穿过B孔,到达P点后,再返回到A孔,则有( )
三个平行金属板a、b、c,ab相距d1,bc相距d2,d2=d1,三个金属板上分别有三个小孔A、B和C,其连线跟板面垂直,三个金属板接到电动势为ε1和ε2的两个电源上,如图所示,ε1<ε2,在A孔的右侧放一个带负电的质点(不计重力),由静止开始释放后,质点将向右运动穿过B孔,到达P点后,再返回到A孔,则有( )| A. | 将b板平行向右移动一小段距离,再释放带电质点,质点仍将运动到P点后返回 | |
| B. | 将b板平行向右移动一小段距离,再释放带电质点,质点将向右运动,并越过P点后返回 | |
| C. | 若将b板平行得向右移动足够远(但不会接触c板),再释放带电质点,质点能够穿过C孔 | |
| D. | 若将带负电质点放在C孔的左侧,由静止释放,它一定能穿过A孔 |

