题目内容
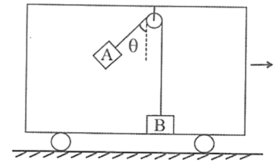
【题目】如图所示,质量为m的木块A和质量为M的木块B用细线捆在一起,木块B与竖直悬挂的轻弹簧相连,它们一起在竖直方向上做简谐运动。在振动中两物体的接触面总处在竖直平面上,设弹簧的劲度系数为k,当它们经过平衡位置时,A、B之间的静摩擦力大小为f0。当它们向下离开平衡位置的位移为x时,A、B间的静摩擦力为fx。细线对木块的摩擦不计。求:
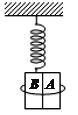
(1)f0的大小;
(2)fx的大小;
【答案】(1)mg(2)![]()
【解析】(1)当物块组振动中通过平衡位置时,两个物块的加速度都是0,其中A受到重力和静摩擦力的作用,所以A受到的静摩擦力大小为f0=mg.
(2)物体A和物体B一起在竖直方向上做简谐振动,回复力F=-kx;
整体的加速度大小为:a=![]() ;
;
对物体A受力分析,受重力和B对A向上的弹力,加速度向上,根据牛顿第二定律,有:
fx-mg=ma
解得:fx=mg+ma=mg+![]()

练习册系列答案
相关题目