��Ŀ����
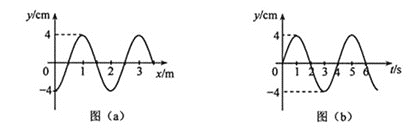
����Ŀ��ͼ1��2��3��ʾ����ֱ���������У��������![]() ��ʱ��
��ʱ��![]() �仯����Χ�ռ�ų�
�仯����Χ�ռ�ų�![]() Ҳ����
Ҳ����![]() �仯���Ӷ��������Ӧ�糡
�仯���Ӷ��������Ӧ�糡![]() �����������߸����ռ������ڣ�
�����������߸����ռ������ڣ�![]() ��
��![]() �ı仯������
�ı仯������![]() ��
��![]() �ı仯�ɽ��ƴ���Ϊ��
�ı仯�ɽ��ƴ���Ϊ��![]() ��ʱ��
��ʱ��![]() �仯ͬ���������������㹻Զ�Ŀռ�����
�仯ͬ���������������㹻Զ�Ŀռ�����![]() ��
��![]() ��
��![]() �ı仯���������
�ı仯���������![]() ��
��![]() �ı仯�����ǵ���ų��仯�������ٶȼ�Ϊ���٣������ͼ���۵Ŀռ������߶Ⱦ��ܴܺ�ģ�ͻ�Ϊͼ��
�ı仯�����ǵ���ų��仯�������ٶȼ�Ϊ���٣������ͼ���۵Ŀռ������߶Ⱦ��ܴܺ�ģ�ͻ�Ϊͼ��![]() �������������һ������ɵ�
�������������һ������ɵ�![]() ��
��![]() ��
��![]() �ı仯�ͺ���
�ı仯�ͺ���![]() ��
��![]() �仯��ЧӦ��ʵ���Կ���ȥ���ڴ�ǰ���£������������
�仯��ЧӦ��ʵ���Կ���ȥ���ڴ�ǰ���£������������
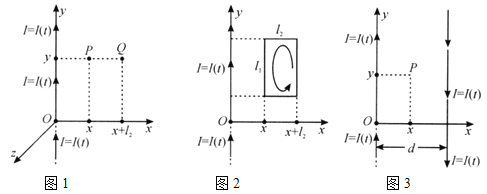
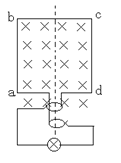
��1��ϵͳ��ͼ1��2��ʾ����![]()
��ͨ���������ж�ͼ1��![]() ƽ����
ƽ����![]() ����Ӧ�糡��ǿ
����Ӧ�糡��ǿ![]() ����������
����������![]() ��
��![]() ��
��![]() ��Ϊ��ķ���
��Ϊ��ķ���
��ͼ2��![]() �����ο�ܵĻ�·�����Ѿ��趨�������·�綯��
�����ο�ܵĻ�·�����Ѿ��趨�������·�綯��![]()
�۽�ͼ1�е�![]() ��
��![]() ������Ӧ�糡��ǿ�Ĵ�С�ֱ��Ϊ
������Ӧ�糡��ǿ�Ĵ�С�ֱ��Ϊ![]() ��
��![]() ������
������![]() ֵ
ֵ
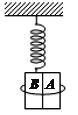
��2����������������������߹��ɵ�ϵͳ��ͼ3��ʾ������![]() ������
������![]() ����Ӧ�糡��ǿ
����Ӧ�糡��ǿ![]() �ķ���ʹ�С
�ķ���ʹ�С
���𰸡���1����![]() ��
��![]() ��
��![]() ��2��
��2��![]() ��������ȡΪ��
��������ȡΪ��![]() �ᷴ��
�ᷴ��
��������
��1������![]() �����ڹ�
�����ڹ�![]() ������
������![]() ������ƽ�е�ƽ���ϣ�ȡһ����
������ƽ�е�ƽ���ϣ�ȡһ����![]() Ϊ�뾶����
Ϊ�뾶����![]() ��Ϊ�������Բ���趨��·���������ͼ��ʾ����ϵͳ����Գ��ԣ���·������Ӧ�糡
��Ϊ�������Բ���趨��·���������ͼ��ʾ����ϵͳ����Գ��ԣ���·������Ӧ�糡![]() �Ľ��������ͼ��
�Ľ��������ͼ��![]() ����һ�µ��ػ�·�����Ҵ�С��ͬ����
����һ�µ��ػ�·�����Ҵ�С��ͬ����![]() �Ļ�·�������õĸ�Ӧ�綯��
�Ļ�·�������õĸ�Ӧ�綯��![]() ����һ���棬����
����һ���棬����![]() �Ĵų�
�Ĵų�![]() �ڸû�·����Χ���ϴ�ͨ����Ϊ�㣬��ͨ���仯ҲΪ�㣬�ݷ����ڵ�Ÿ�Ӧ����Ӧ��
�ڸû�·����Χ���ϴ�ͨ����Ϊ�㣬��ͨ���仯ҲΪ�㣬�ݷ����ڵ�Ÿ�Ӧ����Ӧ��![]() ������ì�ܣ��ʱض���
������ì�ܣ��ʱض���![]() ��
��
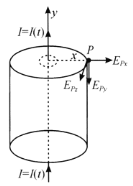
��![]() ����ϵͳ����Գ��ԣ������ͼ1��Բ�����ϸ�����ǿ
����ϵͳ����Գ��ԣ������ͼ1��Բ�����ϸ�����ǿ![]() ��
��![]() �����������С��ͼ��
�����������С��ͼ��![]() ����С��ͬ����ȡһϵ�в�ͬ�뾶
����С��ͬ����ȡһϵ�в�ͬ�뾶![]() ��ͬ��Բ���棬ÿ��Բ�����ϳ�ǿ
��ͬ��Բ���棬ÿ��Բ�����ϳ�ǿ![]() ��
��![]() �������������ͬ����СҲ��ͬ������СӦ��
�������������ͬ����СҲ��ͬ������СӦ��![]() �������С���⽫ʹ������ͼ2�еľ��λ�·������Ӧ�綯��
�������С���⽫ʹ������ͼ2�еľ��λ�·������Ӧ�綯��![]() ���뷨���ڵ�Ÿ�Ӧ����������������
���뷨���ڵ�Ÿ�Ӧ����������������![]()
��![]() ������Գ��ԣ����ͼ1��Բ�����ϸ�����ǿ
������Գ��ԣ����ͼ1��Բ�����ϸ�����ǿ![]() E�ľ������������
E�ľ������������![]() ��Ӧ�ľ�����һ�£����ߴ�СҲ��ͬ�������ͼ1�е�Բ�����ϡ��·ⶥ����Ϊһ��ԲͲ�θ�˹�棬�ϡ�����������
��Ӧ�ľ�����һ�£����ߴ�СҲ��ͬ�������ͼ1�е�Բ�����ϡ��·ⶥ����Ϊһ��ԲͲ�θ�˹�棬�ϡ�����������![]() ͨ������֮��Ϊ�㣬����
ͨ������֮��Ϊ�㣬����![]() ͨ�����ֲ�Ϊ�㣬�������˹Τ��������
ͨ�����ֲ�Ϊ�㣬�������˹Τ��������
![]() ì�ܣ��ʱض���
ì�ܣ��ʱض���![]()
�ھݷ����ڶ��ɣ��ο�����ͼ2����![]() ������
������![]()
���ԣ�![]()
�۾����˹Τ��Ӧ�糡���裬��ϣ�1.1���ʽ����
![]()
��Ϣ٢������ý������
![]()
![]()
����![]()
��2���������Ͽ��ǣ�Զ��Ӧ![]()
������ʽ����![]()
Ϊ���ķ��㣬��![]() ����Ϊ
����Ϊ![]()
![]() Ϊ��ɢ����ϵ��ģ����ɣ�������ʵ
Ϊ��ɢ����ϵ��ģ����ɣ�������ʵ
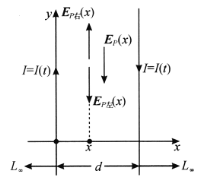
��ͼ��ʾ�������仯��������![]() ���Ҳ�仯��������
���Ҳ�仯��������![]() �ϳɵ�
�ϳɵ�![]() ��������ȡΪ��
��������ȡΪ��![]() �ᷴ��
�ᷴ��
����![]()
![]()
![]()
ʹ��![]()