题目内容
【题目】质点或光滑球以某一角度入射到硬质表面上发生的反跳，通常呈现“反射角等于入射角”的现象．但是对于一种粗糙的硬质橡皮球，当其与硬质表面碰撞且满足动能守恒时，它在反跳过程中却表现出许多奇异的现象，这种粗糙的高弹性人造硬质橡皮球称为超级弹性球，简称为超球．这种超球在硬质表面上的反跳几乎是完全弹性的，用它可以直观地演示粗糙物的弹性碰撞现象．试回答下列问题：
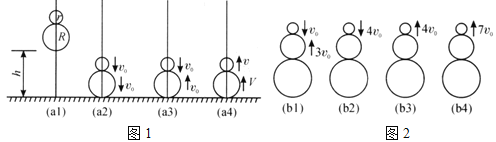
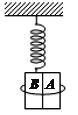
（1）若将一个小超球放在一个大超球的顶上，让这两个超球一起自由下落并撞击地面，就会发现小超球又跳回到空中，如果大超球与小超球的半径之比选择适当，那么小超球将反跳的高度大约是原先下落高度的9倍，如图1所示．若将大超球、小超球和乒乓球紧贴在一起自由下落，如图2所示，如果这些球的质量选择恰当，那么在它们碰撞地面后，乒乓球将反跳的高度几乎是原先下落高度的49倍．试建立力学模型进行说明
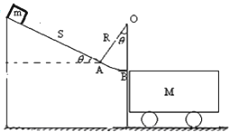
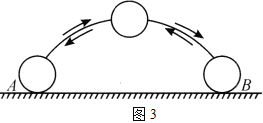
（2）如果超球以一定的速度和绕水平轴旋转的角速度与硬质地面碰撞，旋转的超球在
、
两点之间来回反跳，如图3所示．试说明发生这种现象的条件
【答案】（1）说明见解析 （2）说明见解析
【解析】
（1）在大超球碰撞地面之前，两超球均自由下落，它们之间未发生碰撞，大超球先与地面相碰撞，随后立即与小超球发生碰撞，假设大超球与地面以及超球间的碰撞都是完全弹性的．两超球自由下落结束时，都有向下的速度，由机械能守恒可得
；大超球与地面弹性碰撞后，速度大小不变，方向向上．设大超球与小超球弹性碰撞后的速度大小分别为
和
，且方向向上．由动量守恒和机械能守恒，可得
①
②
式中，
为大超球的质量；
为小超球的质量
由式①与式②，可解得
，
③
碰撞后小超球以初速度为竖直向上运动，由机械能守恒可得小超球反跳的高度：
④
即得
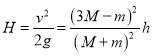⑤
若选择大超球半径为小超球半径的10倍，即
，则
．于是，由式⑤得到
对于题图2所示的三个紧贴的球，设由上至下三个球的质量分别为
、
和
，且满足
．根据前面的分析，当大球与地面碰撞后，立即与球发生碰撞，由式③可知，当球以相对于地面
的速度反跳时，小球正以速度
下落题图2-b1．在相对球为瞬时静止的惯性系里，小球相对于球以速度
与球相碰撞（题图2-b2）．由于
，碰撞后球相对于球以速度反跳（题图2-b3），即小球相对于地面以速度
反跳（题图2-b4）．因此，小球反跳的高度
为
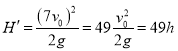⑥
（2）首先，讨论旋转超球在硬质地面上的碰撞问题．假设碰撞是完全弹性的，且碰撞瞬间超球与地面接触点处没有相对滑动，但受到摩擦力的作用，同时忽略重力的影响．为讨论方便，碰撞前的运动状态用下标“0”表示，第一次碰撞后用“1”、第二次碰撞后用“2”表示，依此类推．
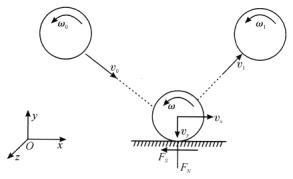
取超球运动的平面为
平面，如图所示，设超球的质量为，半径为
，在第一次碰撞前超球质心的速度（以
和
表示速度的两个分量）和旋转角速度
（超球对于通过质心的
轴的角速度）；碰撞后的速度分量为
和
，角速度为
，设接触点处的摩擦力为
，法向力为
，作用时间为
．
根据质点的动量定理，在
方向有
⑦
根据动量矩定理，对通过质心的轴有
⑧
其中，
为超球对于通过质心的轴的转动惯量，对于均质实心球，有
此外，对于弹性碰撞，因摩擦力不做功，由机械能守恒定律可得
⑨
考虑到完全弹性碰撞，可知
⑩
由式⑦和式⑧，可得
再由式⑨，并利用式⑩与式，得到
现在，要实现在
、
两点之间来回反跳，要求、两处反跳后的运动状态左右对称，因此反跳前后超球质心的速度与角速度应满足：
，
，
将式代入式中，得到
可见，若超球以角速度旋转，同时以
的水平分速度与地面碰撞，则反跳后超球以
再次与地面相撞，这样超球就来回反跳
