��Ŀ����
17�� ��ͼ��ʾ��ˮƽ���õ������⻬ƽ�н�������a��b��c������Ϊd=1m������a��c����һ����Ϊm=1kg�Ľ�����MN�����뵼��ʼ�����ýӴ������ĵ���r=2��������ĵ�����Բ��ƣ��ڵ���b��c���һ����ΪR=2���ĵ��ݣ�����ac���һ������ر�������װ�÷��ڴŸ�Ӧǿ��B=2T��ǿ�ų��У��ų�����ֱ����ƽ�����£��ֶ�MNʩ��һˮƽ���ҵ�����F��ʹ���Ӿ�ֹ��ʼ�˶���������ʩ�ӵ�ˮƽ�������ʺ�ΪP=20W������t=1sʱ�䣬�����ٶȴﵽ2m/s�������������ʩ�ӵ�ˮƽ�����������Ժ���˶������а����ܻ��������λ��Ϊ���٣�
��ͼ��ʾ��ˮƽ���õ������⻬ƽ�н�������a��b��c������Ϊd=1m������a��c����һ����Ϊm=1kg�Ľ�����MN�����뵼��ʼ�����ýӴ������ĵ���r=2��������ĵ�����Բ��ƣ��ڵ���b��c���һ����ΪR=2���ĵ��ݣ�����ac���һ������ر�������װ�÷��ڴŸ�Ӧǿ��B=2T��ǿ�ų��У��ų�����ֱ����ƽ�����£��ֶ�MNʩ��һˮƽ���ҵ�����F��ʹ���Ӿ�ֹ��ʼ�˶���������ʩ�ӵ�ˮƽ�������ʺ�ΪP=20W������t=1sʱ�䣬�����ٶȴﵽ2m/s�������������ʩ�ӵ�ˮƽ�����������Ժ���˶������а����ܻ��������λ��Ϊ���٣�
���� ����ˮƽ�������������������˶�������ţ�ٵڶ����ɺͼ��ٶȵĶ���ʽa=$\frac{��v}{��t}$��ϣ��õ��ٶȵı仯����λ�Ʊ仯���Ĺ�ϵʽ������ͼ��ɵý⣮
��� �⣺����ˮƽ������������ٶ�Ϊvʱ���ٶ�Ϊa��ȡ����ʱ���t�о���ȡ����Ϊ��������ţ�ٵڶ����ɵ�
-BIL=ma
��I=$\frac{Bdv}{R+\frac{1}{2}r}$��a=$\frac{��v}{��t}$
������-$\frac{{B}^{2}{d}^{2}v}{R+\frac{1}{2}r}$=m•$\frac{��v}{��t}$
�� ��-$\frac{{B}^{2}{d}^{2}v}{R+\frac{1}{2}r}$����t=m•��v
������͵ã�$\sum_{\;}^{\;}$��-$\frac{{B}^{2}{d}^{2}v}{R+\frac{1}{2}r}$����t=$\sum_{\;}^{\;}$m•��v
ʽ��v��t=��x��$\sum_{\;}^{\;}$v��t=$\sum_{\;}^{\;}$��x=x
���-$\frac{{B}^{2}{d}^{2}x}{R+\frac{1}{2}r}$=m��0-v��
����� $\frac{{2}^{2}��{1}^{2}��x}{2+\frac{1}{2}��2}$=1��2
��� x=1.5m
�𣺰����ܻ��������λ��Ϊ1.5m��
���� �����dz�ȥF��������DZ����ֱ���˶����������˶�ѧ��ʽ��λ�ƣ���Ҫ����Ԫ������������Ǽ��ٶȵĶ���ʽ��

 ��ͼ��ʾ��λ��ˮƽ�����ϵ����P����Ϊ2m���ɿ�������ֵ�����������Ϊm�����Q�������ӻ��ֵ�P�͵�Q������������ˮƽ�ģ���֪Q��P֮���Լ�P������֮��Ķ�Ħ���������Ǧ̣����ֵ��������������ϵ�Ħ�������ƣ�����һˮƽ���ҵ���F��Qʹ���������˶�����F�Ĵ�СΪ��������
��ͼ��ʾ��λ��ˮƽ�����ϵ����P����Ϊ2m���ɿ�������ֵ�����������Ϊm�����Q�������ӻ��ֵ�P�͵�Q������������ˮƽ�ģ���֪Q��P֮���Լ�P������֮��Ķ�Ħ���������Ǧ̣����ֵ��������������ϵ�Ħ�������ƣ�����һˮƽ���ҵ���F��Qʹ���������˶�����F�Ĵ�СΪ��������| A�� | 3��mg | B�� | 4��mg | C�� | 5��mg | D�� | 6��mg |

| A�� | �����ܵ���֧������С | B�� | �����ܵ���Ħ������� | ||
| C�� | �������ܵĺ������ | D�� | ���ԶԵ��������������� |
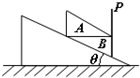 ��ͼ��ʾ�����Ϊ��=30��Ĺ⻬б���Ϲ̶�����ֱ�⻬����P��������ͬ�ĺ����Ϊֱ�������ε������A��B������б���뵵��֮�䣬��A��B��ĽӴ���ˮƽ����A��B��ѹ����B��б���ѹ��֮��ӦΪ��������
��ͼ��ʾ�����Ϊ��=30��Ĺ⻬б���Ϲ̶�����ֱ�⻬����P��������ͬ�ĺ����Ϊֱ�������ε������A��B������б���뵵��֮�䣬��A��B��ĽӴ���ˮƽ����A��B��ѹ����B��б���ѹ��֮��ӦΪ��������| A�� | 2��1 | B�� | $\sqrt{3}$��2 | C�� | $\sqrt{3}$��1 | D�� | $\sqrt{3}$��4 |

 ��ͼ��ʾ���ڱڹ⻬�İ����������뾶ΪR��һ��С����Ϊ�ʵ㣩����������ˮƽ��������Բ���˶���С��������������������ֱ����ɦȽǣ���С��������Բ���˶��Ľ��ٶ�Ϊ$\sqrt{\frac{g}{Rcos��}}$��
��ͼ��ʾ���ڱڹ⻬�İ����������뾶ΪR��һ��С����Ϊ�ʵ㣩����������ˮƽ��������Բ���˶���С��������������������ֱ����ɦȽǣ���С��������Բ���˶��Ľ��ٶ�Ϊ$\sqrt{\frac{g}{Rcos��}}$�� ��ͼ����ʾ�������㹻����ֱ��������MN��PQƽ�з��������Ϊ�ȵľ�Եб���ϣ���������ΪL��M��P����������ֵΪR�ĵ��裮һ������Ϊm�ľ���ֱ������ab�����������ϣ����뵼�촹ֱ������װ�ô��ڴŸ�Ӧǿ��ΪB����ǿ�ų��У��ų�����ֱб�����£������˵ĵ���Ϊr����ab���ص����ɾ�ֹ��ʼ�»�������ͽ����˽Ӵ����ã���������֮���Ħ����
��ͼ����ʾ�������㹻����ֱ��������MN��PQƽ�з��������Ϊ�ȵľ�Եб���ϣ���������ΪL��M��P����������ֵΪR�ĵ��裮һ������Ϊm�ľ���ֱ������ab�����������ϣ����뵼�촹ֱ������װ�ô��ڴŸ�Ӧǿ��ΪB����ǿ�ų��У��ų�����ֱб�����£������˵ĵ���Ϊr����ab���ص����ɾ�ֹ��ʼ�»�������ͽ����˽Ӵ����ã���������֮���Ħ����