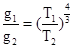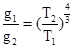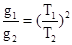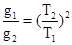题目内容
太阳围绕银河系中心的运动可视为匀速圆周运动，其运动速度约为地球公转速度的7倍，轨道半径约为地球公转轨道半径的2×109倍，为了粗略估算银河系中恒星的数目，可认为银河系中所有恒星的质量都集中在银河系中心，且银河系中恒星的平均质量约等于太阳质量，则银河系中恒星数目约为
| A．109 | B．1011 | C．1013 | D．1015 |
B
解析试题分析：据题意，环绕天体围绕中心天体做匀速圆周运动，万有引力定律提供向心力，则有：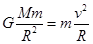
，整理得：
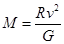，设恒星总质量为M，太阳质量为
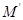，则有：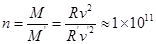
，故B选项正确。
考点：本题考查万有引力定律。
阅读快车系列答案据《科技日报》报道，2020年前我国将发射8颗海洋系列卫星，包括4颗海洋水色卫星、2颗海洋动力环境卫星和2颗海陆雷达卫星，以加强对黄岩岛、钓鱼岛及西沙群岛全部岛屿附近海域的监测。设海陆雷达卫星绕地球做匀速圆周运动的轨道半径是海洋动力环境卫星的n倍，则在相同的时间内（ ）
| A．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的n倍 |
| B．海陆雷达卫星和海洋动力环境卫星到地球球心的连线扫过的面积相等 |
C．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的 倍 |
D．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的 倍 |
质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动。已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的（ ）
A．线速度  | B．角速度ω= |
C．运行周期 | D．向心加速度 |
海王星有13颗已知的天然卫星。现认为海卫二绕海王星沿圆轨道匀速运转，已知海卫二的质量2.0×l019kg，轨道半径为5.5×106km，运行的周期为360天，万有引力常量G=6.67×l0－1lN·m2/kg2。则海王星的质量大约为
| A．1.0×1017kg | B．l.0×l026kg | C．2.0×l01lkg | D．2.0×l019kg |
我国“二炮”的一系列导弹，在“北斗”定位系统的引导下，能实现精确打击移动目标和固定目标。假设从地面上A点发射一枚远程弹道导弹，仅在地球引力作用下，沿ACB椭圆轨道飞行击中地面目标B， C为轨道的远地点，距地面高度为h，若ACB轨迹长恰好为整个椭圆的一半。已知地球半径为R，地球质量为M，引力常量为G。则下列结论正确的是 （ ）
A．导弹在C点的速度大于  |
| B．地球的球心位于导弹椭圆轨道的一个焦点上 |
C．导弹在C点的加速度等于 |
| D．导弹从A点到B点的飞行时间等于导弹飞行周期的一半 |
如图所示，“嫦娥一号”探月卫星进入月球轨道后，首先在椭圆轨道Ⅰ上运动，P、Q两点是轨道Ⅰ的近月点和远月点，Ⅱ是卫星绕月做圆周运动的轨道，轨道Ⅰ和Ⅱ在P点相切，关于该探月卫星的运动，下列说法正确的是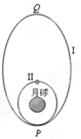
| A．卫星在轨道Ⅰ上运动周期大于在轨道Ⅱ上运动的周期 |
| B．卫星由轨道Ⅰ进入轨道Ⅱ必须要在P点加速 |
| C．卫星在轨道Ⅰ上运动时，P点的速度小于Q点的速度 |
| D．卫星在轨道Ⅰ上运动时，P点的加速度小于Q点的加速度 |
为了探测X星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1. 随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，此时登陆舱的质量为m2，则（ ）
A．X星球的质量为M= |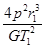
B．X星球表面的重力加速度为gx= |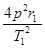
C．登陆舱在半径为r2轨道上做圆周运动的周期为 |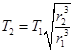
D．登陆舱在r1与r2轨道上运动时的速度大小之比为 |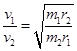
甲、乙为两颗地球卫星，其中甲为地球同步卫星，乙的运行高度低于甲的运行高度，两卫星轨道均可视为圆轨道。以下判断正确的是( )
| A．甲的周期小于乙的周期 |
| B．乙的速度大于第一宇宙速度 |
| C．甲的加速度小于乙的加速度 |
| D．甲在运行时能经过北极的正上方 |