题目内容
7.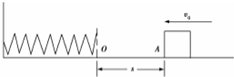 如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )| A. | 弹簧的最大压缩量为$\frac{{v}_{0}^{2}}{2μg}$ | |
| B. | 弹簧的最大压缩量为$\frac{{v}_{0}^2}{4μg}$ | |
| C. | 弹簧获得的最大弹性势能为$\frac{1}{2}mv$${\;}_{0}^{2}$ | |
| D. | 弹簧获得的最大弹性势能为$\frac{1}{4}$mv${\;}_{0}^{2}$ |
分析 求解本题的关键是明确对物体、弹簧、地面组成的系统应用能量守恒定律即可求解.
解答 解:AB、物体受到的滑动摩擦力大小为f=μmg,设弹簧的最大压缩量为x,则物块从A点再回到A点的过程中,由能量守恒有
2μmg(x+s)=$\frac{1}{2}$mv02,弹簧的最大压缩量 x=$\frac{{v}_{0}^{2}}{4μg}$-s,故A、B错误;
CD、从A点到弹簧最大压缩量的过程中,EPm+μmg(s+x)=$\frac{1}{2}$mv02,因此最大弹性势能为EPm=$\frac{1}{4}$mv02,故C错误、D正确.
故选:D
点评 注意摩擦生热公式为Q=fs,其中s是物体相对接触面发生的相对路程;对系统应用能量守恒定律求解较简便.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
17.每年的低温雨雪冰冻都会造成我国部分地区高压输电线严重损毁.为消除高压输电线上的凌冰,有人设计了这样的融冰思路:利用电流的热效应除冰.若在正常供电时,高压线上输电电压为U,电流为I,热耗功率为P;除冰时,输电线上的热耗功率需变为16P,则除冰时(认为输电功率和输电线电阻不变)( )
| A. | 输电电流为16I | B. | 输电电压为4U | C. | 输电电流为$\frac{I}{4}$ | D. | 输电电压为$\frac{U}{4}$ |
18.一颗烟花弹从地面竖直向上发射,到达的最大高度为20m,不计空气阻力,取重力加速度g=10m/s2,则烟花弹发射的初速度大小为( )
| A. | 5m/s | B. | 10m/s | C. | 20m/s | D. | 40m/s |
2. 如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )
如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )
 如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )
如图所示,处于真空的点电荷a、b、c、d的电荷量分别为+q、+q、-q、-q,四边形abcd为菱形,∠a=60°.1、2、3、4分别为所在边的中点,其对应边的电场强度大小分别为E1、E2、E3、E4,对应的电势分别为φ1、φ2、φ3、φ4,则下列说法正确的是( )| A. | E1=E3、φ1=φ3 | B. | E2=E4、φ2=φ4 | C. | E1=E3、φ1>φ3 | D. | E2=E4、φ2>φ4 |
 如图所示,A、B两平行金属板之间的电势差为U,一重力不计的带负电微粒,在A、B之间电场的作用下,从A板处由静止开始运动,穿过B板上的小孔后,进入水平放置的C、D两平行金属板之间,入射的速度方向沿两板的中心线,微粒最后刚好从D板的右边缘射出.已知C、D板的长度为L,两板之间的距离为$\frac{L}{8}$,问:
如图所示,A、B两平行金属板之间的电势差为U,一重力不计的带负电微粒,在A、B之间电场的作用下,从A板处由静止开始运动,穿过B板上的小孔后,进入水平放置的C、D两平行金属板之间,入射的速度方向沿两板的中心线,微粒最后刚好从D板的右边缘射出.已知C、D板的长度为L,两板之间的距离为$\frac{L}{8}$,问: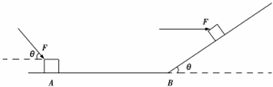 如图所示,水平面与斜面在B点对接,一质量为1kg的物块放在水平面上A点,用与水平面成θ=53°向下的恒力推物块,物块以3m/s2的加速度向右运动,A、B间距为6m,物块到B点后滑上斜面,不计撞击带来的能量损失,物块滑上斜面后推力大小不变,方向变成水平,物块与水平面和斜面之间的动摩擦因数均为0.5,求:
如图所示,水平面与斜面在B点对接,一质量为1kg的物块放在水平面上A点,用与水平面成θ=53°向下的恒力推物块,物块以3m/s2的加速度向右运动,A、B间距为6m,物块到B点后滑上斜面,不计撞击带来的能量损失,物块滑上斜面后推力大小不变,方向变成水平,物块与水平面和斜面之间的动摩擦因数均为0.5,求: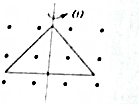
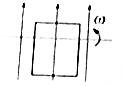


 如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?
如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?