题目内容
16. 如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?
如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?
分析 根据题意求出气体的状态参量,气体发生等温变化,应用玻意耳定律可以求出气体的体积,然后求出活塞下移的距离.
解答 解:气体初状态压强:p1=p0-$\frac{G}{S}$,体积:V1=dS,
气体末状态的压强:p2=p0-$\frac{G+{G}_{1}}{S}$,体积:V2=(d+x)S,
气体发生等温变化,由玻意耳定律得:p1V1=p2V2,
即:(p0-$\frac{G}{S}$)dS=(p0-$\frac{G+{G}_{1}}{S}$)(d+x)S,
解得:x=$\frac{{G}_{1}d}{{p}_{0}S-G-{G}_{1}}$;
答:活塞再次稳定静止时下移的距离为:$\frac{{G}_{1}d}{{p}_{0}S-G-{G}_{1}}$.
点评 本题考查了求活塞移动的距离,分析清楚物体状态变化过程,知道气体发生等温变化是正确解题的关键,求出气体的状态参量,应用玻意耳定律可以解题.

练习册系列答案
相关题目
6. 如图所示,总重为G的考拉母子静止在倾斜角为α的树树上,则树枝对考拉母子的总作用力为( )
如图所示,总重为G的考拉母子静止在倾斜角为α的树树上,则树枝对考拉母子的总作用力为( )
 如图所示,总重为G的考拉母子静止在倾斜角为α的树树上,则树枝对考拉母子的总作用力为( )
如图所示,总重为G的考拉母子静止在倾斜角为α的树树上,则树枝对考拉母子的总作用力为( )| A. | Gsinα | B. | Gcosα | C. | 小于G | D. | G |
7.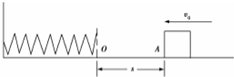 如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
 如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )| A. | 弹簧的最大压缩量为$\frac{{v}_{0}^{2}}{2μg}$ | |
| B. | 弹簧的最大压缩量为$\frac{{v}_{0}^2}{4μg}$ | |
| C. | 弹簧获得的最大弹性势能为$\frac{1}{2}mv$${\;}_{0}^{2}$ | |
| D. | 弹簧获得的最大弹性势能为$\frac{1}{4}$mv${\;}_{0}^{2}$ |
11. 图甲中的变压器为理想变压器,原、副线圈的匝数n1与n2之比为5:1.变压器的原线圈如图乙所示的正弦交变电流,两个20Ω的定值电阻串联接在副线圈两端.电压表
图甲中的变压器为理想变压器,原、副线圈的匝数n1与n2之比为5:1.变压器的原线圈如图乙所示的正弦交变电流,两个20Ω的定值电阻串联接在副线圈两端.电压表 为理想电表,则( )
为理想电表,则( )
 图甲中的变压器为理想变压器,原、副线圈的匝数n1与n2之比为5:1.变压器的原线圈如图乙所示的正弦交变电流,两个20Ω的定值电阻串联接在副线圈两端.电压表
图甲中的变压器为理想变压器,原、副线圈的匝数n1与n2之比为5:1.变压器的原线圈如图乙所示的正弦交变电流,两个20Ω的定值电阻串联接在副线圈两端.电压表 为理想电表,则( )
为理想电表,则( )| A. | 原线圈的输入功率为40W | B. | 电压表 的示数为20V 的示数为20V | ||
| C. | 副线圈中电流的方向每秒改变10次 | D. | 流经原、副线圈的电流之比为1:5 |
8. 如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )
如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )
 如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )
如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{3}$mgR | C. | $\frac{1}{2}$mgR | D. | mgR |
8.如图,在同一竖直平面内,距地面不同高度的地方,以不同的水平速度同时抛出两个小球,则( )

| A. | 两球一定不能在空中相遇 | |
| B. | 两球落地时间可能相等 | |
| C. | 两球抛出到落地的水平距离有可能相等 | |
| D. | 两球运动的水平距离与抛出点的高度无关 |

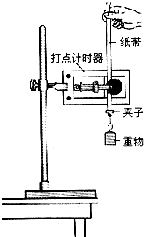 某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤:
某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤: