题目内容
12.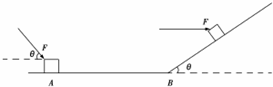 如图所示,水平面与斜面在B点对接,一质量为1kg的物块放在水平面上A点,用与水平面成θ=53°向下的恒力推物块,物块以3m/s2的加速度向右运动,A、B间距为6m,物块到B点后滑上斜面,不计撞击带来的能量损失,物块滑上斜面后推力大小不变,方向变成水平,物块与水平面和斜面之间的动摩擦因数均为0.5,求:
如图所示,水平面与斜面在B点对接,一质量为1kg的物块放在水平面上A点,用与水平面成θ=53°向下的恒力推物块,物块以3m/s2的加速度向右运动,A、B间距为6m,物块到B点后滑上斜面,不计撞击带来的能量损失,物块滑上斜面后推力大小不变,方向变成水平,物块与水平面和斜面之间的动摩擦因数均为0.5,求:(1)推力F的大小;
(2)物块在斜面上滑行的最大距离.
分析 (1)根据牛顿第二定律求得合外力,结合受力分析求出分力F;
(2)结合(1)中的知识求得物体到达B点的速度,利用牛顿第二定律和运动学公式求解即可,
解答 解:(1)物块的加速度为3m/s2,根据牛顿第二定律,解得:F合=ma=3N,对物体受力分析,竖直方向:N=Fsinθ+mg,水平方向:Fcosθ-f=F合,又f=μN,
将三式联立得:Fcosθ-μFsinθ-μmg=ma,
代入数据:F×0.6-0.5×F×0.8-0.5×1×10=3,
解得:F=40N
(2)物体在斜面上运动,有运动学公式得:${v}^{2}-{v}_{0}^{2}=2ax$,
代入数据得:v2=2×3×6,
解得:v=6m/s,
对物体受力分析得:物体在斜面上运动时:mgsinθ+f-Fcosθ=ma2,
垂直斜面方向上:N=mgcosθ+Fsinθ,又:f=μN,
代入数据解得:10×0.8+0.5×10×0.6+0.5×40×0.8-40×0.6=a2,
得:a2=3m/s2,方向向下;
物体在斜面上做匀减速运动,设滑行的最大距离为x2,
有运动学公式得:${v}^{2}-{v}_{0}^{2}=2ax$2,
代入数据:0-62=2×(-3)x2,
解得:x2=6m.
答:(1)推力F的大小为40N,
(2)物块在斜面上滑行的最大距离为6m
点评 本题是牛顿第二定律的典型应用题,用好牛顿第二定律和运动学公式是解题的关键,特别注重加速度的方向.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7.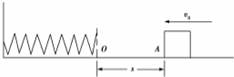 如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
 如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )
如图所示,轻弹簧一端固定在挡板上,质量为m的物体以初速度v0沿水平面向左运动,起始点A与轻弹簧自由端O的距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后弹簧被压缩,之后物体被向右反弹,回到A点时的速度刚好为零,则( )| A. | 弹簧的最大压缩量为$\frac{{v}_{0}^{2}}{2μg}$ | |
| B. | 弹簧的最大压缩量为$\frac{{v}_{0}^2}{4μg}$ | |
| C. | 弹簧获得的最大弹性势能为$\frac{1}{2}mv$${\;}_{0}^{2}$ | |
| D. | 弹簧获得的最大弹性势能为$\frac{1}{4}$mv${\;}_{0}^{2}$ |
17.下列说法不正确的是 ( )
| A. | 铯137进行β衰变时,往往同时释放出γ射线,γ射线具有很强的穿透能力,甚至能穿透几厘米的铅板 | |
| B. | 紫外线照射到金属锌板表面时能够发生光电效应,当增大紫外线的照射强度时,从锌板表面逸出的光电子的最大初动能也随之增大. | |
| C. | ${\;}_{92}^{285}$U吸收光子后会裂变,发生链式反应,释放核能 | |
| D. | 由玻尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| E. | 用能量为12eV的电子碰撞处于基态的氢原子,氢原子可能吸收其部分能量而跃迁到激发态 |
2.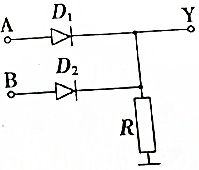 如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
 如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )| A. | A=0,B=0时,Y=1 | B. | A=0,B=1时,Y=0 | C. | A=1、B=0时,Y=1 | D. | A=1、B=1时,Y=1 |
 汽车由静止开始在平直的公路上行驶,0~30s内汽车的速度随时间变化的图线如图所示,求:
汽车由静止开始在平直的公路上行驶,0~30s内汽车的速度随时间变化的图线如图所示,求: