题目内容
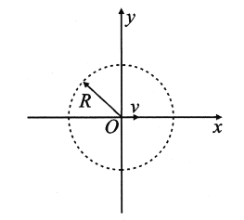
【题目】如图所示为一种质谱仪的工作原理图，圆心角为90°的扇形区域OPQ中存在着磁感应强度大小为B、方向垂直纸面向外的匀强磁场，所有带电粒子经加速电压U加速后从小孔C射出，由磁场边界OP上N点垂直OP进入磁场区域，然后均从边界OQ射出，已知ON＝l.
(1) 若由静止开始加速的某种粒子X从边界OQ射出时速度方向与OQ垂直，其轨迹如图中实线所示，求该粒子的比荷
；
(2) 若由静止开始加速的另一种粒子Y比荷是X粒子的
，求该粒子在磁场区域中运动的时间t；
(3) 由于有些粒子具有垂直于加速电场方向的初速度，导致粒子束以小发散角(纸面内)从C射出，这些粒子在CN方向上的分速度均相同，求CN长度d调节为多少时，可使一束X粒子从边界OQ射出后能在磁场区域右侧D点处被全部收集到(点D与C关于∠POQ的角平分线OH对称，部分粒子轨迹如图中虚线所示)．
【答案】（1）
（2）
（3）l
【解析】
(1) 粒子在电场中加速的末速度为
，由动能定理可得：
在磁场中有牛顿第二定律可得：
由几何知识可知，粒子的轨道半径为：
联立以上方程解得：
(2) 
粒子在磁场中的轨迹如图所示：
由(1)可得粒子在磁场中的轨迹半径为:
由图甲可得：
由三角函数可知：
所以在磁场中中运动的时间为：
联立以上方程解得：
(3) 设发散最远的粒子为
，该粒子的轨迹如图虚线所示：
由题意可得：
该粒子的轨迹半径为
，由牛顿第二定律可得：
得
由
联立上式可得
由几何知识可得：
联立以上方程解得：
练习册系列答案
相关题目
