题目内容
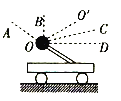
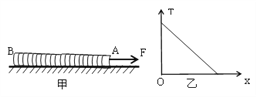
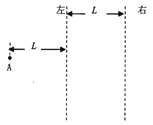
【题目】如图所示,倾角为θ=30°的光滑斜面与光滑水平面间有光滑小圆弧衔接.将小球甲从斜面上高h=0.05m处的A点由静止释放,同时小球乙从距离B点L=0.4m的C点以速度V0沿水平面向左匀速运动.甲开始运动后经过t=1s刚好追上乙.求:小球乙的速度V0 . (g取10m/s2)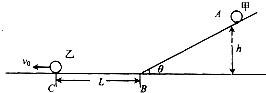
【答案】解:设小球甲在光滑斜面上运动的加速度为a,运动时间为t1,运动到B处时的速度为v1,
从B处到追上小球乙所用时间为t2,则a=gsin 30°=5 m/s2
由 ![]() 得
得 ![]() =0.2 s
=0.2 s
v1=at1=1 m/s
t2=t﹣t1=0.8 s
v0t+L=v1t2
代入数据解得:v0=0.4 m/s
答:小球乙的速度为 0.4 m/s.
【解析】讨论追及、相遇的问题,其实质就是分析讨论两物体在相同时间内能否到达相同的空间位置问题,抓住位移之间的关系根据运动学基本公式即可求解.
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系的相关知识点,需要掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值才能正确解答此题.

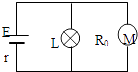
【题目】在测量电源的电动势和内阻的实验中,由于所用的电压表(视为理想电压表)的量程较小,某同学设计了如图所示的实物电路.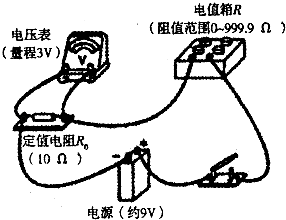
①实验时,应先将电阻箱的电阻调到 . (选填“最大值”、“最小值”或“任意值”)
②改变电阻箱的阻值R,分别测出阻值R0=10Ω的定值电阻两端的电压U,下列两组R的取值方案中,比较合理的方案是 . (选填l或2)
方案编号 | 电阻箱的阻值R/Ω | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
③根据实验数据描点,绘出的 ![]() 图象是一条直线.若直线的斜率为k,在
图象是一条直线.若直线的斜率为k,在 ![]() 坐标轴上的截距为b,则该电源的电动势E= , 内阻r=(用k、b和R0表示).
坐标轴上的截距为b,则该电源的电动势E= , 内阻r=(用k、b和R0表示).