题目内容
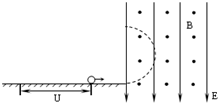 如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )| A、小球可能带正电 | ||||||
B、小球做匀速圆周运动的半径为r=
| ||||||
C、小球做匀速圆周运动的周期为T=
| ||||||
| D、若电压U增大,则小球做匀速圆周运动的周期增加 |
分析:小球在竖直平面内做匀速圆周运动,故重力等于电场力,即洛伦兹力提供向心力,所以mg=Eq,由于电场力的方向与场强的方向相反,
根据qvB=
,解得r=
,运动周期T=
,在加速电场中根据动能定理qU=
mv2.
根据qvB=
| mv2 |
| r |
| mv |
| qB |
| 2πr |
| v |
| 1 |
| 2 |
解答:解:A、小球在竖直平面内做匀速圆周运动,故重力等于电场力,即洛伦兹力提供向心力,所以mg=Eq,由于电场力的方向与场强的方向相反,故小球带负电,故A错误;
B、由于洛伦兹力提供向心力,故有;qvB=
,
解得:r=
,
又由于qU=
mv2,
解得:v=
所以:r=
,故B正确;
C、由于洛伦兹力提供向心力做圆周运动,故有运动周期为:
T=
=
=
,故C正确;
D、由于洛伦兹力提供向心力做圆周运动,故有运动周期为:
T=
=
,显然运动周期与加速电压无关,故D错误;
故选:BC.
B、由于洛伦兹力提供向心力,故有;qvB=
| mv2 |
| r |
解得:r=
| mv |
| qB |
又由于qU=
| 1 |
| 2 |
解得:v=
|
所以:r=
| 1 |
| B |
|
C、由于洛伦兹力提供向心力做圆周运动,故有运动周期为:
T=
| 2πr |
| v |
| 2πm |
| qB |
| 2πE |
| Bg |
D、由于洛伦兹力提供向心力做圆周运动,故有运动周期为:
T=
| 2πr |
| v |
| 2πm |
| qB |
故选:BC.
点评:本题考查了带电粒子在复合场中的圆周运动的周期公式,轨道半径公式,带电粒子在电场中的加速运动和动能定理,本题综合性较强,选项D容易出错.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( ) 如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )





