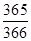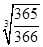题目内容
某星球的半径为R,在其表面上方高度为aR的位置,以初速度v0水平抛出一个金属小球,水平射程为bR,a、b均为数值极小的常数,则这个星球的第一宇宙速度为( )
A. | B.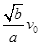 | C. | D. |
A
解析试题分析:设该星球表面重力加速度为g,小球落地时间为t,抛出的金属小球做平抛运动,根据平抛运动规律得aR=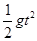 bR=v0t,联立以上两式解得g=
bR=v0t,联立以上两式解得g=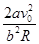 ,第一宇宙速度即为该星球地表卫星线速度,根据地表卫星重力充当向心力得mg=m
,第一宇宙速度即为该星球地表卫星线速度,根据地表卫星重力充当向心力得mg=m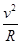 ,所以第一宇宙速度v=
,所以第一宇宙速度v=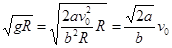 ,故选项A正确。
,故选项A正确。
考点:平抛运动 牛顿第二定律 第一宇宙速度

2013年12月2日1时30分,我国成功发射了“嫦娥二号”探月卫星,12月6日17时47分顺利进入环月轨道.若该卫星在地球、月球表面的重力分别为G1、G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
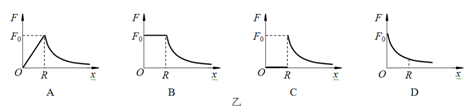
A.月球表面处的重力加速度为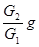 |
B.月球与地球的质量之比为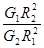 |
C.卫星沿近月球表面轨道上做匀速圆周运动的周期为 |
D.月球与地球的第一宇宙速度之比为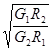 |
2010年10月1日下午,中国探月二期工程先导星“嫦娥二号”在西昌点火升空,准确入轨,10月9日“嫦娥二号”卫星成功实施第三次近月制动后,进入距离月球表面100公里的环月圆轨道,是嫦娥二号卫星工作期间一个主要使用的工作轨道。已知月球的质量为地球质量的1/81,月球半径为地球半径的3/11,地球上的第一宇宙速度为7.9km/s,地表的重力加速度为9.8m/s2,地球半径为6.4×106m,则该卫星在100公里环月轨道上运动的速度和加速度最接近的是
| A.0.16km/s,0.44m/s2 | B.0.36km/s,1.6m/s2 |
| C.1.6km/s,1.6m/s2 | D.1.6km/s,0.44 m/s2 |
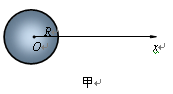
如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上,设地球质量为M、半径为R.下列说法正确的是( )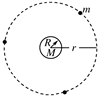
A.地球对一颗卫星的引力大小为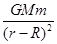 |
B.一颗卫星对地球的引力大小为 |
C.两颗卫星之间的引力大小为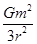 |
D.三颗卫星对地球引力的合力大小为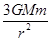 |
有些卫星因能量耗尽而报废,成为太空垃圾,所以被称为“垃圾卫星”。“轨道康复者”是“垃圾卫星”的救星,被称为“太空110”,它可在太空中给“垃圾卫星”补充能量,延长卫星的使用寿命。假设“轨道康复者”绕地球做匀速圆周运动时的轨道半径为地球同步卫星轨道半径的五分之一,其运动方向与地球自转方向一致,轨道平面与地球赤道平面重合。下列判断正确的是 ()
| A.“轨道康复者”的加速度是地球同步卫星加速度的25倍 |
B.“轨道康复者”的周期是地球同步卫星周期的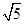 倍 倍 |
| C.站在赤道上的人用仪器观察到“轨道康复者”向东运动 |
| D.“轨道康复者”要在原轨道上加速才能“拯救”更低轨道上的卫星 |
1970年4月24日,我国自行设计、制造的第一颗人造地球卫星“东方红一号”发射成功,开创了我国航天事业的新纪元.“东方红一号”的运行轨道为椭圆轨道,其近地点M和远地点N的高度分别为439km和2384km,则 ( )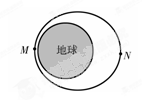
| A.卫星在N点的速度小于7.9km/s |
| B.卫星在N点的速度大于7.9km/s |
| C.卫星在M点的加速度大于N点的加速度 |
| D.卫星在N点若再适当加速则可进入过N点的圆轨道运行 |
冥王星绕太阳的公转轨道是个椭圆,公转周期为T0,其近日点到太阳的距离为a,远日点到太阳的距离为b,半短轴的长度为c,如图所示.若太阳的质量为M,万有引力常量为G,忽略其他行星对它的影响,则( ).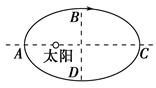
| A.冥王星从A―→B―→C的过程中,速率逐渐变小 |
B.冥王星从A―→B所用的时间等于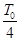 |
| C.冥王星从B―→C―→D的过程中,万有引力对它先做正功后做负功 |
D.冥王星在B点的加速度为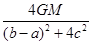 |
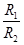 =
=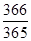
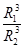 =
=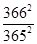
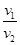 =
=