题目内容
3.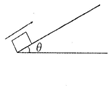 如图所示,在倾角为θ=37°的足够长的固定斜面底端,一小物块以某一初速度沿斜面上滑,一段时间后返回到出发点,若物块上滑所用时间t1和下滑所用时间t2的大小关系满足t1:t2=1:$\sqrt{5}$,(取g=10m/s2,sin37°=0.6,cos37°=0.8),试求:
如图所示,在倾角为θ=37°的足够长的固定斜面底端,一小物块以某一初速度沿斜面上滑,一段时间后返回到出发点,若物块上滑所用时间t1和下滑所用时间t2的大小关系满足t1:t2=1:$\sqrt{5}$,(取g=10m/s2,sin37°=0.6,cos37°=0.8),试求:(1)上滑加速度a1与下滑加速度a2的大小之比;
(2)物块和斜面之间的动摩擦因数;
(3)若斜面倾角变为60°,并改变斜面粗糙程度,小物块上滑的同时用水平向右的推力F作用在物块上,发现物块匀减速上滑过程中加速度与推力大小无关,求此时加速度大小(结果保留3位有效数字).
分析 (1)由题意知,物块上滑和下滑的位移大小相等,利用匀变速直线运动的位移公式求出加速度大小之比;
(2)分别对物块上滑和下滑受力分析,根据牛顿第二定律列方程联立求出物块和斜面之间的动摩擦因数;
(3)对小物块上滑时受力分析,应用牛顿第二定律和力的平衡条件求出加速度的表达式,根据加速度与推力无关求出动摩擦因数,然后求出加速度大小.
解答 解:(1)物块向上做匀减速直线运动,向下做初速度为零的匀加速直线运动,由题意知,它们的位移大小相等,由匀变速直线运动的位移公式得:
$\frac{1}{2}$a1${t}_{1}^{2}$=$\frac{1}{2}$a2${t}_{2}^{2}$,
解得:$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{t}_{2}^{2}}{{t}_{1}^{2}}$=$\frac{5}{1}$.
(2)由牛顿第二定律得:
物块上滑时,mgsin37°+μmgcos37°=ma1,
物块下滑时,mgsin37°-μmgcos37°=ma2,
解得:μ=0.5. (3)物体上滑时受力分析如图所示:
(3)物体上滑时受力分析如图所示:
由牛顿第二定律得,mgsin60°+μ′N-Fcos60°=ma,
由平衡条件得:N=Fsin60°+mgcos60°,
整理得:mgsin60°+μ′Fsin60°+μ′mgcos60°-Fcos60°=ma,
因为a与F无关,所以,μFsin60°-Fcos60°=0,
解得:μ′=cot60°=$\frac{\sqrt{3}}{3}$;
a=gsin60°+μ′gcos60°=$\frac{20\sqrt{3}}{3}$m/s2≈11.5m/s2.
答:(1)上滑加速度a1与下滑加速度a2的大小之比为5:1;
(2)物块和斜面之间的动摩擦因数为0.5;
(3)此时加速度大小为11.5m/s2.
点评 本题考查了学生对匀变速直线运动规律和牛顿第二定律的掌握和应用,关键是对物块在斜面上进行受力分析,运用牛顿第二定律并结合运动学公式即可正确解题.注意情景发生改变,要重新进行受力分析.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 如图所示,M、N和P为“验证动量守恒定律”实验中小球的落点,已知入射球质量为m1,被碰球质量为m2,如果碰撞中动量守恒,则有( )
如图所示,M、N和P为“验证动量守恒定律”实验中小球的落点,已知入射球质量为m1,被碰球质量为m2,如果碰撞中动量守恒,则有( )| A. | m1•($\overrightarrow{OP}$-$\overrightarrow{OM}$)=m2•$\overrightarrow{ON}$ | B. | m1•($\overrightarrow{OP}$-$\overrightarrow{OM}$)=m2•$\overrightarrow{O′N}$ | C. | m1•($\overrightarrow{OP}$+$\overrightarrow{OM}$)=m2•$\overrightarrow{O′N}$ | D. | m1•$\overrightarrow{OP}$=m2•($\overrightarrow{O′N}$+$\overrightarrow{OM}$) |
| A. | 伽利略推断:从同一炮台水平发射的炮弹,如果不受空气阻力,不论它们能射多远,在空中飞行的时间都一样 | |
| B. | 古希腊学者托勒密在《天文学大成》中提出了日心说 | |
| C. | 开普勒发现了行星运动三定律和万有引力定律 | |
| D. | 卡文迪许通过扭秤实验精确测量了引力常量,并且预言了海王星的存在 |
 如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )
如图所示为由二极管构成的逻辑电路,A、B为输入端,Y为输出端,高电位用真值“1”表示,低电位用真值“0”表示,则( )| A. | A=0,B=0时Y=0 | B. | A=1,B=0时Y=1 | C. | A=0,B=1时Y=1 | D. | A=1,B=1时Y=1 |
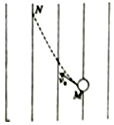 电子枪是加速电子轰击靶屏发光的一种装置,它发射出具有一定能量、一定束流以及速度和角度的电子束.电子束中某个电子只在电场力作用下从M点运动到N点的轨迹如图中虚线所示,图中一组平行实线可能是等势面也可能是电场线,则以下说法正确的是( )
电子枪是加速电子轰击靶屏发光的一种装置,它发射出具有一定能量、一定束流以及速度和角度的电子束.电子束中某个电子只在电场力作用下从M点运动到N点的轨迹如图中虚线所示,图中一组平行实线可能是等势面也可能是电场线,则以下说法正确的是( )| A. | 若图中实线是电场线,电子在M点的速度较大 | |
| B. | 若图中实线是电场线,M点的电势比N点低 | |
| C. | 不论图中实线是电场线还是等势面,电子在M点动能小 | |
| D. | 不论图中实线是电场线还是等势面,M点的场强都比N点小 |
| A. | 线速度 | B. | 向心加速度 | C. | 周期 | D. | 动能 |
 图中虚线为匀强电场中与场强方向垂直的等间距平行直线,两粒子M、N质量相等,所带电荷的绝对值也相等,现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )
图中虚线为匀强电场中与场强方向垂直的等间距平行直线,两粒子M、N质量相等,所带电荷的绝对值也相等,现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )| A. | N从O点运动至a点时克服电场力做功 | |
| B. | N在a点的速率小于M在c点的速率 | |
| C. | M带正电荷,N带负电荷 | |
| D. | M从O点运动至b点时电场力对它做的功为零 |
 ,让小球从C点由静止释放.其沿细杆由C经B向A运动的
,让小球从C点由静止释放.其沿细杆由C经B向A运动的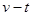 图像如图乙所示.且已知小球运动到B点时,速度图像的切线斜率最大(图中标出了该切线)下列说法正确的是( )
图像如图乙所示.且已知小球运动到B点时,速度图像的切线斜率最大(图中标出了该切线)下列说法正确的是( )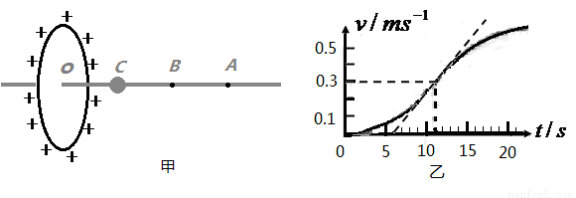
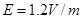
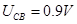
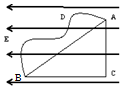 如图所示,在场强为E的匀强电场中有相距为L的两点A、B,连线AB与电场线的夹角为θ,将一电荷量为q的正电荷从A点移到B点.若沿直线AB移动该电荷,电场力做功W=qELcosθ,AB两点间的电势差UAB=ELcosθ.
如图所示,在场强为E的匀强电场中有相距为L的两点A、B,连线AB与电场线的夹角为θ,将一电荷量为q的正电荷从A点移到B点.若沿直线AB移动该电荷,电场力做功W=qELcosθ,AB两点间的电势差UAB=ELcosθ.