题目内容
9. 如图所示,质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分,当靶盒A进入相互作用区时便受到水平向左的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒每次发射一颗水平速度v0=50m/s,质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.今约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.
如图所示,质量M=0.40kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分,当靶盒A进入相互作用区时便受到水平向左的恒力F=20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒每次发射一颗水平速度v0=50m/s,质量m=0.10kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短.今约定,每当靶盒A停在或到达O点时,都有一颗子弹进入靶盒A内.(1)当第一颗子弹进入靶盒A后,靶盒A离开O点最大距离为多少?
(2)当第三颗子弹进入靶盒A后,靶盒A从离开O点到又回到O点所经历时间为多少?
(3)求发射器B至少发射几颗子弹后,靶盒A能在相互作用区内运动且距离不超过0.2m?
分析 (1)第一颗子弹进入靶盒A后,根据碰撞过程系统动量守恒列出等式,再运用动能定理求解.
(2)根据题意,A在的恒力F的作用返回O点时第二颗子弹正好打入,由于A的动量与第二颗子弹动量大小相同,方向相反,故第二颗子弹打入后,A将静止在O点.由系统动量守恒和动能定理求解.
(3)n颗子弹入射靶盒后,靶盒速度为Vn,离开O点的最大距离为Sn,则根据动量守恒定律有(M+nm)Vn=mV0,再结合动能定理求解.
解答 解:(1)设第一颗子弹进入靶盒A后,子弹与靶盒A共同速度为υ1.
根据碰撞过程系统动量守恒,有mυ0=(m+M)υ1…①
设A离开O点的最大距离为s1,根据动能定理有:-Fs1=0-$\frac{1}{2}$(m+M)${v}_{1}^{2}$…②
由①、②式得s1=1.25m…③
(2)根据题意,A在恒力F作用下返回O点时第二颗子弹打入,由于A的动量与第二颗子弹动量大小相同、方向相反,
第二颗子弹打入后A将静止在O点.设第三颗子弹打入A后,它们的共同速度为υ3
由系统动量守恒:mυ0=(M+3m)υ3…④
设A从离开O点到又回到O点经历时间为t,且碰后A运动方向为正方向,
由动量定理得:-F×$\frac{1}{2}$t=0-(M+3m)υ3…⑤
由④、⑤两式得:t=0.5s…⑥
(3)设B至少发射n颗子弹,且碰后A的速度为υn
由系统动量守恒:mυ0=(M+nm)υn…⑦
由动能定理:-Fsn=0-$\frac{1}{2}$×(M+nm)${v}_{n}^{2}$…⑧
根据题意:sn<0.2m …⑨
由⑦、⑧、⑨式得:n>27,所以B至少发射28颗子弹.
答:(1)当第一颗子弹进入靶盒A后,靶盒A离开O点最大距离为1.25m.
(2)当第三颗子弹进入靶盒A后,靶盒A从离开O点到又回到O点所经历时间为0.5s.
(3)发射器B至少发射28颗子弹后,靶盒A在相互作用区内运动的距离不超过0.2m.
点评 本题可以等效于碰撞模型;对于碰撞过程,其基本规律动量守恒定律要掌握牢固,并能正确运用.能把动量守恒定律和动能定理结合应用.

 名校课堂系列答案
名校课堂系列答案 如图1所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出如图2滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图1所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出如图2滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )| A. | 小滑块的质量为0.1kg | |
| B. | 轻弹簧原长为0.2m | |
| C. | 弹簧最大弹性势能为0.5J | |
| D. | 小滑块的重力势能与弹簧的弹性势能总和最小为0.4J |
 如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-2m和x=12m处,两列波的速度均为v=4m/s,两波源的振幅均为A=2cm.图示为t=0时刻两列波的图象(传播方向如图所示),此时刻平衡位置处于x=2m和x=8m的P、Q两质点刚开始振动.质点M的平衡位置处于x=5m处,关于各质点运动情况判断正确的是( )
如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-2m和x=12m处,两列波的速度均为v=4m/s,两波源的振幅均为A=2cm.图示为t=0时刻两列波的图象(传播方向如图所示),此时刻平衡位置处于x=2m和x=8m的P、Q两质点刚开始振动.质点M的平衡位置处于x=5m处,关于各质点运动情况判断正确的是( )| A. | 两列波相遇过后振幅仍然为2 cm | B. | t=1s时刻,质点M的位移为-4cm | ||
| C. | t=1s时刻,质点M的位移为+4cm | D. | t=0.75s时刻,质点P、Q都运动到M点 |
| A. | 飞船受到的万有引力逐渐增大,线速度逐渐减小 | |
| B. | 飞船的向心加速度逐渐增大,周期逐渐减小,线速度和角速度都逐渐增大 | |
| C. | 飞船的动能、重力势能和机械能都逐渐减小 | |
| D. | 重力势能逐渐减小,动能逐渐增大,机械能逐渐减小 |
 如图所示是氢原子能级图,大量处于n=4激发态的氢原子向低能级跃迁时,一共可以辐射出6种不同频率的光子.其中巴耳末系是指氢原子由高轨道向第2轨道跃迁释放的光子.下列有关跃迁过程的说法正确的是( )
如图所示是氢原子能级图,大量处于n=4激发态的氢原子向低能级跃迁时,一共可以辐射出6种不同频率的光子.其中巴耳末系是指氢原子由高轨道向第2轨道跃迁释放的光子.下列有关跃迁过程的说法正确的是( )| A. | 6种光子中有两种属巴耳末系 | |
| B. | 6种光子中频率最高的是从n=4激发态直接跃迁到基态时产生的 | |
| C. | 若氢原子从n=2能级跃迁到基态能使锌板发生光电效应,则氢原子从n=3能级跃迁到n=2能级也一定能使锌板发生光电效应 | |
| D. | 使n=4能级的氢原子电离至少要0.85eV的能量 |
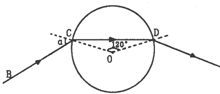 如图所示,真空中有一半径为R、圆心为O的均匀玻璃球,频率一定的细激光束在真空中沿BC传播,从C点经折射进入玻璃球,并经出射点D折射出去,已知∠COD=120°,玻璃对该激光的折射率为$\sqrt{3}$,则下列说法中正确的是( )
如图所示,真空中有一半径为R、圆心为O的均匀玻璃球,频率一定的细激光束在真空中沿BC传播,从C点经折射进入玻璃球,并经出射点D折射出去,已知∠COD=120°,玻璃对该激光的折射率为$\sqrt{3}$,则下列说法中正确的是( )| A. | 激光束在C点的入射角α=60° | |
| B. | 此激光束在玻璃中穿越的时间为t=$\frac{3R}{c}$ | |
| C. | 一个光子在穿过玻璃球的过程中能量逐渐变小 | |
| D. | 改变入射角α的大小,细激光束可能在球表面D处发生全反射 |
| A. | B=2T | B. | B≤2T | ||
| C. | B≥2T | D. | 以上情况都有可能 |

 一根玻璃管封闭,另一端开口,内用10厘米长的水银柱封闭住一段空气,空气柱长5厘米,则当玻璃管水平放置时,空气柱长5.66厘米,如图所示,已知大气压强p0=76厘米汞柱.
一根玻璃管封闭,另一端开口,内用10厘米长的水银柱封闭住一段空气,空气柱长5厘米,则当玻璃管水平放置时,空气柱长5.66厘米,如图所示,已知大气压强p0=76厘米汞柱.