题目内容
12.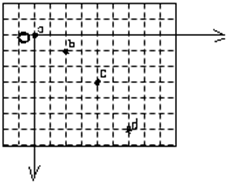 如图所示为小球做平抛运动的闪光照片的一部分,小方格的边长L=2.50cm.在oxy坐标系中记录了小球做平抛运动途中的几个位置,标记为a、b、c、d四点,a点的坐标设为(0.00,0.00)cm,已知重力加速度g取10.00m/s2,则(所有计算结果保留两位小数)
如图所示为小球做平抛运动的闪光照片的一部分,小方格的边长L=2.50cm.在oxy坐标系中记录了小球做平抛运动途中的几个位置,标记为a、b、c、d四点,a点的坐标设为(0.00,0.00)cm,已知重力加速度g取10.00m/s2,则(所有计算结果保留两位小数)(1)照相机的闪光频率是20Hz
(2)小球平抛的初速度V0=1m/s
(3)小球经过b位置的竖直分速度Vby=0.75m/s
(4)小球经过b位置的速度Vb=1.25m/s
(5)小球做平抛运动抛出点距a点距离为:x=2.5 cm.
分析 根据连续相等时间内的位移之差是一恒量求出相等的时间间隔,从而得出闪光的频率,根据水平位移和时间间隔求出小球平抛运动的初速度.根据某段时间内的平均速度等于中间时刻的瞬时速度求出小球经过b位置的竖直分速度,结合平行四边形定则求出小球经过b位置的速度.
根据速度时间公式求出抛出点到b点的时间,从而得出抛出点到b点的水平位移,确定抛出点与a点的水平位移.
解答 解:(1)在竖直方向上,根据△y=L=gT2得,T=$\sqrt{\frac{L}{g}}=\sqrt{\frac{2.5×1{0}^{-2}}{10}}s=0.05s$,
则闪光的频率f=$\frac{1}{T}=\frac{1}{0.05}Hz=20Hz$.
(2)小球平抛运动的初速度${v}_{0}=\frac{2L}{T}=\frac{0.05}{0.05}m/s=1m/s$.
(3)小球经过b位置的竖直分速度${v}_{by}=\frac{3L}{2T}=\frac{3×2.50×1{0}^{-2}}{0.1}$m/s=0.75m/s.
(4)根据平行四边形定则知,小球经过b点的速度${v}_{b}=\sqrt{{{v}_{0}}^{2}+{{v}_{by}}^{2}}$=$\sqrt{1+0.7{5}^{2}}$m/s=1.25m/s.
(5)抛出点到b点的时间${t}_{b}=\frac{{v}_{yb}}{g}=\frac{0.75}{10}s=0.075s$,则抛出点到b点的水平位移xb=v0tb=1×0.075m=0.075m=7.5cm,
所以小球做平抛运动抛出点距a点距离为x=7.5-5cm=2.5cm.
故答案为:20,1,0.75,1.25,2.5.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解,难度不大.

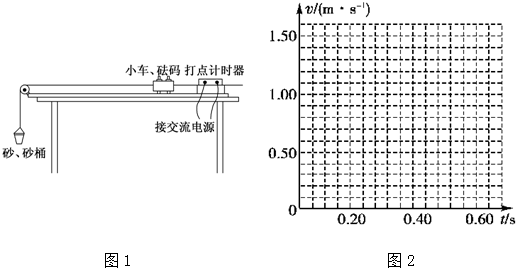
①请通过计算,在下表空格内填入合适的数据(计算结果保留到小数点后两位);
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
| 各计数点的速度/(m•s-1) | 0.50 | 0.70 | 0.90 | 1.10 | 1.51 |
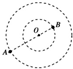 “双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小于两个星球之间的距离,而且双星系统一般远离其他天体.如图所示,相距为L的A、B两恒星绕共同的圆心O做圆周运动,A、B的质量分别为m1、m2,周期均为T.若有间距也为L的双星C、D,C、D的质量分别为A、B的两倍,则( )
“双星体系”由两颗相距较近的恒星组成,每个恒星的半径远小于两个星球之间的距离,而且双星系统一般远离其他天体.如图所示,相距为L的A、B两恒星绕共同的圆心O做圆周运动,A、B的质量分别为m1、m2,周期均为T.若有间距也为L的双星C、D,C、D的质量分别为A、B的两倍,则( )| A. | A、B运动的轨道半径之比为$\frac{{m}_{1}}{{m}_{2}}$ | B. | A、B运动的速率之比为$\frac{{m}_{1}}{{m}_{2}}$ | ||
| C. | C运动的速率为A的2倍 | D. | C、D运动的周期均为$\frac{\sqrt{2}}{2}$T |
| A. | 电流方向改变 | B. | 磁通量为零 | ||
| C. | 圈中磁通量的变化率最大 | D. | 线圈边切割磁感线 |
| A. | 甲、乙两分子间距离一定小于r0 | |
| B. | 甲、乙两分子间距离一定大于r0 | |
| C. | 甲、乙两分子质量一定不等且甲的质量大于乙的质量 | |
| D. | 甲、乙两分子运动速率一定不等且甲的速率大于乙的速率 |
| A. | 汽车做匀加速运动 | B. | 汽车做匀减速运动 | ||
| C. | 汽车的位移增加 | D. | 汽车的速度变化不均匀 |

