��Ŀ����
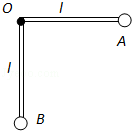
��ͼ��ʾ��������ͬ��l��˹���һ��ֱ����֧�ܣ���A�˹̶�����Ϊ2m��С��B�˹̶�����Ϊm��С��֧�ܿ���O������ֱ����������ת���ִ�OB��ֱ��OAˮƽ����ֹ�ͷ�֧�ܣ�����˵������ȷ���ǣ�������
A.A����͵�ʱ�ٶ�Ϊ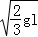
B.�ӿ�ʼ�� A����͵�Ĺ����У�֧�ܶ�B�����Ĺ�Ϊ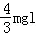
C.��֧���°�45��ʱ��A��B����ȸ�ʱ����A���ٶ����
D.��֧�ܴ������ҷ��ذڶ�ʱ��A��һ���ܻص���ʼ�߶�

A.A����͵�ʱ�ٶ�Ϊ
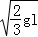
B.�ӿ�ʼ�� A����͵�Ĺ����У�֧�ܶ�B�����Ĺ�Ϊ
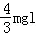
C.��֧���°�45��ʱ��A��B����ȸ�ʱ����A���ٶ����
D.��֧�ܴ������ҷ��ذڶ�ʱ��A��һ���ܻص���ʼ�߶�
ABD
���������AB��������ɵ�ϵͳ��е���غ㣬����ϵͳ�Ļ�е���غ���ʽ�������A����͵�ʱ�ٶȣ���B���ݶ��ܶ�����ʽ���֧�ܶ�B�����Ĺ�������ϵͳ�Ļ�е���غ���ʽ��ʽ�õ������ٶ����ת���ǶȵĹ�ϵ�������ٶ���������������ϵͳ���ɻ�е���غ����֧�ܴ������ҷ��ذڶ�ʱA��ﵽ����߸߶ȣ�
�⣺A��A����͵�ʱ��A��B������ٶȴ�СΪv������ϵͳ�Ļ�е���غ㶨�ɵã�
mg?2l��mgl=
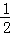 ��m+2m��v2
��m+2m��v2��ã�v=
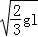 ����A��ȷ��
����A��ȷ��B������B�ӿ�ʼ��A����͵�Ĺ����У��ɶ��ܶ����ã�
��mgl+W=
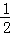 mv2����v=
mv2����v=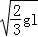 ������֧�ܶ�B�����Ĺ�Ϊ��W=
������֧�ܶ�B�����Ĺ�Ϊ��W=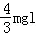 ����B��ȷ��
����B��ȷ��C����֧������ת���н�Ϊ��ʱ���ɻ�е���غ�ã�
2mglsin�ȩ�mgl��1��cos�ȣ�=
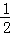 ��m+2m��v2
��m+2m��v2�ã�v2=
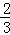 gl[��2sin��+cos�ȣ���1]
gl[��2sin��+cos�ȣ���1]������ѧ֪ʶ��֪������=90�㩁arctan0.5ʱ��v���C����
D������ϵͳ�Ļ�е�غ��֪����֧�ܴ������ҷ��ذڶ�ʱ��A��һ���ܻص���ʼ�߶ȣ���D��ȷ��
��ѡ��ABD
����������ؼ�ץס��������ɵ������е���غ㣬֪�������ٶȴ�С��ȣ�������ѧ֪ʶ�����ٶ�����������

��ϰ��ϵ�д�
 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�����Ŀ
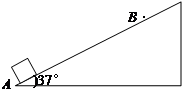
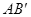 ��ʾ���Դ�A���ɾ�ֹ�ͷŸ�Сľ�飬��ľ�����ս�ͣ���ڣ�����ľ��ͨ��ת�۵�B���
��ʾ���Դ�A���ɾ�ֹ�ͷŸ�Сľ�飬��ľ�����ս�ͣ���ڣ�����ľ��ͨ��ת�۵�B���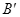 ���������ʧ���� ��
���������ʧ���� ��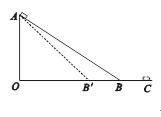



 ��W
��W ����W
����W