题目内容
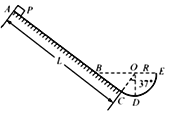
【题目】（15分）如题图所示，在半径为a的圆柱空间中（图中圆为其横截面）充满磁感应强度大小为B的均匀磁场，其方向平行于轴线远离读者．在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1．6a的刚性等边三角形框架ΔDEF，其中心O位于圆柱的轴线上．DE边上S点（
）处有一发射带电粒子的源，发射粒子的方向皆在题图中截面内且垂直于DE边向下。发射粒子的电量皆为q（＞0），质量皆为m，但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失（不能与圆柱壁相碰），电量也无变化，且每一次碰撞时速度方向均垂直于被碰的边。试问：
（1）带电粒子经多长时间第一次与DE边相碰？
（2）带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点？
（3）这些粒子中，回到S点所用的最短时间是多少？
【答案】（1）
（2）
（3）
【解析】
试题
（1）带电粒子（以下简称粒子）从S点垂直于DE边以速度v射出后，在洛伦兹力作用下做匀速圆周运动
得
①
粒子在磁场中做圆周运动的周期为：
将①式代入，得：
②
粒子第一次与DE边相碰：
（2）
、
的长度应是Rn的奇数倍即：
(
＝1，2，3，…) ③
此时为Rn的奇数倍的条件自然满足。
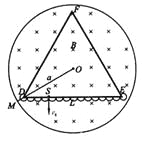
而粒子要能绕过顶点与ΔDEF的边相碰，则粒子作圆周运动的半径R不能太大，如图题解图，必须有：
④
由图中的几何关系计算可知：
⑤
由③④⑤得：n≥4
由此结论及①、③两式可得：
⑥
（3）最短时间时应取n=4，所需时间为：
⑦
以②式代入得：⑧
练习册系列答案
相关题目
