题目内容
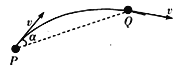
【题目】在xoy坐标平面的第一象限内存在着垂直平面向外的匀强磁场，如图所示，从y轴上M点（
）垂直y轴射入一质量为m，电荷量为q的正电荷，速率为v，恰能从横轴上的N点（
）射出磁场。不计电荷的重力。
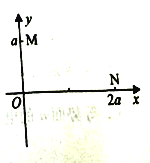
（1）求磁场的磁感应强项；
（2）求从N点射出时速度方向与x轴夹角的正切值；
（3）如果把第一象限的磁场收缩为一个圆形磁场，磁感应强度变为原来的3倍，要使该正电荷还以原来的方向经过N点，求圆形磁场区域的最小面积。
【答案】（1）
（2）
（3）
【解析】（1）设粒子的轨道半径为R，有几何关系得 R2=(2a)2+(R-a)2
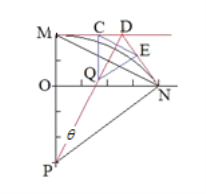
解得： R=2.5a
解得： 
（2）速度偏向角等于粒子转过的圆心角
（3）因为
所以
若要粒子经过N点的速度方向不变，则粒子的轨迹应为如图所示的CE之间的一段弧长。若要所加圆磁场的面积最小，应以弦长CE为直径，所得的圆磁场面积最小
由题目条件已知 
相似
由相似比得 
相似
由相似比得 
所以
代入数据得 
所求圆的面积
练习册系列答案
相关题目
