题目内容
2.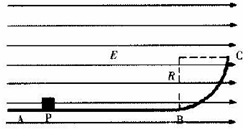 如图所示,光滑、绝缘的水平轨道AB与四分之一圆弧轨道BC平滑连接,并均处于水平向右的匀强电场中,已知匀强电场的场强E=5×103V/m,圆弧轨道半径R=0.4m.现有一带电量q=+2×10-5C、质量m=5×10-2kg的物块(可视为质点)从距B端s=1m处的P点由静止释放,加速运动到B端,再平滑进人圆弧轨道BC,重力加速度g=10m/s2,求:
如图所示,光滑、绝缘的水平轨道AB与四分之一圆弧轨道BC平滑连接,并均处于水平向右的匀强电场中,已知匀强电场的场强E=5×103V/m,圆弧轨道半径R=0.4m.现有一带电量q=+2×10-5C、质量m=5×10-2kg的物块(可视为质点)从距B端s=1m处的P点由静止释放,加速运动到B端,再平滑进人圆弧轨道BC,重力加速度g=10m/s2,求:(1)物块在水平轨道上加速运动的时间t和到达B点的速度vB的大小
(2)物块刚进人圆弧轨道时受到的支持力NB的大小.
(3)物块在BC段运动速度vm的大小.
分析 (1)带电体在光滑水平轨道AB上由电场力作用下,从静止开始做匀加速直线运动,由牛顿第二定律可求出加速度大小,由运动学公式可算出时间和到B端的速度大小.
(2)由带电体运动到B端的速度,及牛顿第二定律可求出物块刚进入圆弧轨道时受到的支持力NB的大小.
(3)对从B向右的过程,设物体YU圆心连线与竖直方向的夹角为θ,根据动能定理列式,结合数学知识求解速度最大值.
解答 解:(1)设带电体在水平轨道上运动的加速度大小为a,根据牛顿第二定律得:
qE=ma
解得:$a=\frac{qE}{m}=\frac{{2×1{0^{-5}}×5×1{0^3}}}{{5×1{0^{-2}}}}=2m/{s^2}$
由s=$\frac{1}{2}a{t}^{2}$,得:$t=\sqrt{\frac{2s}{a}}=\sqrt{\frac{2×1}{2}}s=1s$
带电体运动到B端的速度大小为:vB=at=2m/s.
(2)设带电体运动到圆弧形轨道B端时受轨道的支持力为FN,根据牛顿第二定律有:
${N_B}-mg=\frac{mv_B^2}{R}$
代入数据解得:NB=1N
(3)对从B向右的过程,设物体YU圆心连线与竖直方向的夹角为θ,根据动能定理,有:
$-mg(R-Rcosθ)+qERsinθ=\frac{1}{2}m{v^2}-\frac{1}{2}mv_B^2$
解得:${v}_{B}=\sqrt{1.6(sinθ+5cosθ)-4}$=$\sqrt{1.6\sqrt{26}(\frac{1}{\sqrt{26}}sinθ+\frac{5}{\sqrt{26}}cosθ)-4}$=$\sqrt{1.6\sqrt{26}sin(θ+α)-4}$
其中:$sinθ=\frac{5}{\sqrt{26}}$
故物块在BC段运动速度为:vm=$\sqrt{1.6\sqrt{26}-4}$m/s≈2.04m/s
答:(1)物块在水平轨道上加速运动的时间是1s,到达B点的速度vB的大小为2m/s.
(2)物块刚进人圆弧轨道时受到的支持力NB的大小是1N.
(3)物块在BC段运动速度vm的大小约为2.04m/s.
点评 前两问较为基础,利用牛顿第二定律与运动学公式相结合进行解答,也可以运用动能定理和运动学公式结合求解;第三问涉及极值问题,可以根据数学知识求解极值.

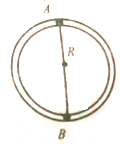 如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动,今对上方小球A施加微小扰动,两球开始运动后,下列说法正确的是( )
如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动,今对上方小球A施加微小扰动,两球开始运动后,下列说法正确的是( )| A. | 轻杆转到水平位置时两球的加速度大小相等 | |
| B. | 轻杆转到竖直位置时两球的加速度大小不相等 | |
| C. | 运动过程中A球速度的最大值为$\sqrt{\frac{4gR}{3}}$ | |
| D. | 当A球运动到最低点时,两小球对轨道作用力的合力大小为$\frac{13}{3}$mg |
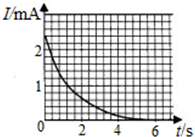
| A. | 3.28C | B. | 3.28×10-3C | C. | 5.76C | D. | 5.76×10-3C |
 用与竖直方向成α=37°斜向右上方,大小为F=50N的推力把一个质量为m=5kg的木块压在粗糙竖直墙上保持静止.求墙对木块的弹力大小N和墙对木块的摩擦力f.(sin37°=0.6,cos37°=0.8,g=10m/s2)
用与竖直方向成α=37°斜向右上方,大小为F=50N的推力把一个质量为m=5kg的木块压在粗糙竖直墙上保持静止.求墙对木块的弹力大小N和墙对木块的摩擦力f.(sin37°=0.6,cos37°=0.8,g=10m/s2)