��Ŀ����
7���������������IJ���̽��������������˸������ʶ�������Ա�������϶�N�š����������Ա���������ϲ��һ����Ϊm�����������ΪF1����������������ͬһ����ʱ������ΪF2����1��������������ת��������Ӱ�죬����������Ӧ������뾶����������Ӧ������뾶֮��Ϊ���
��2�����������ת���ɺ��ԣ�ͬʱ�����ɰ뾶ΪR�����壬��������ת�����ڶ��
���� ��1������������������������$F=G\frac{mM}{{R}^{2}}$��������ֵ����ɵã�
��2�����������壬�������������������������Ϊ������������תʱ�����������ݴ����������ת�����ڼ��ɣ�
��� �⣺��1��������ɵ����������������������У�
�ڳ�����У�${F}_{1}=G\frac{mM}{{R}_{1}^{2}}$ ��
��������${F}_{2}=G\frac{mM}{{R}_{2}^{2}}$ ��
�����ɢ٢���ʽ�ɵã�$\frac{{R}_{1}}{{R}_{2}}$=$\sqrt{\frac{{F}_{2}}{{F}_{1}}}$
��2���ڳ����������������ת����������������֮���ṩ������ת������������������������ת��������Ϊ�㣬������������������ȣ������У�
${F}_{2}-{F}_{1}=mR\frac{4{��}^{2}}{{T}^{2}}$
�ɵ�������ת������T=$2��\sqrt{\frac{mR}{{F}_{2}-{F}_{1}}}$
�𣺣�1��������������ת��������Ӱ�죬����������Ӧ������뾶����������Ӧ������뾶֮��Ϊ$\sqrt{\frac{{F}_{2}}{{F}_{1}}}$��
��2�����������ת���ɺ��ԣ�ͬʱ�����ɰ뾶ΪR�����壬��������ת������Ϊ$2��\sqrt{\frac{mR}{{F}_{2}-{F}_{1}}}$��
���� ����������ת��������Ӱ�죬���������������������������������ɵĹ�ʽ������������תʱ��������������������Ϊ������Բ���˶�����������

 ��У����ϵ�д�
��У����ϵ�д�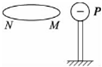 ��ͼ��ʾ��������У���һ����Ե��������������P�������������ھ�Ե�������˵ĵ�ɣ�����˵������ȷ���ǣ�������
��ͼ��ʾ��������У���һ����Ե��������������P�������������ھ�Ե�������˵ĵ�ɣ�����˵������ȷ���ǣ�������| A�� | M�˴����磬N�˴����� | B�� | M�˴����磬N�˴����� | ||
| C�� | M�˵ĵ��������N�˵ĵ���� | D�� | N�˵ĵ��������M�˵ĵ���� |
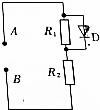 ��ͼ��ʾ����·�еĵ���R1�����R2����ֵ��ΪR����R1������DΪ��������ܣ��������ɿ����㣬�������ɿ����������A��B���ijAһ���ҽ�����ѹʱ�������R2�ϵĵ�ѹ��ЧֵΪ5$\sqrt{10}$V���ɴ˿�֪��һ���ҽ�����ѹ�����ֵΪ��������
��ͼ��ʾ����·�еĵ���R1�����R2����ֵ��ΪR����R1������DΪ��������ܣ��������ɿ����㣬�������ɿ����������A��B���ijAһ���ҽ�����ѹʱ�������R2�ϵĵ�ѹ��ЧֵΪ5$\sqrt{10}$V���ɴ˿�֪��һ���ҽ�����ѹ�����ֵΪ��������| A�� | 10V | B�� | 10$\sqrt{2}$V | C�� | 20V | D�� | 20$\sqrt{2}$V |
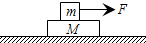 ��ͼ��ʾ������ΪM�ij�ľ��λ�ڹ⻬ˮƽ���ϣ�����Ϊm����龲ֹ�ڳ�ľ���ϣ�����֮��Ļ���Ħ������Ϊ�̣��ֶ����mʩ��ˮƽ���ҵĺ���F��������F����ijһ�ٽ���ֵ����ľ������齫������Ի������������ٶȴ�СΪg������볤ľ��֮������Ħ������������֮��Ļ���Ħ�����������F���ٽ���ֵΪ��������
��ͼ��ʾ������ΪM�ij�ľ��λ�ڹ⻬ˮƽ���ϣ�����Ϊm����龲ֹ�ڳ�ľ���ϣ�����֮��Ļ���Ħ������Ϊ�̣��ֶ����mʩ��ˮƽ���ҵĺ���F��������F����ijһ�ٽ���ֵ����ľ������齫������Ի������������ٶȴ�СΪg������볤ľ��֮������Ħ������������֮��Ļ���Ħ�����������F���ٽ���ֵΪ��������| A�� | ��mg | B�� | ��Mg | C�� | ��mg��1+$\frac{m}{M}$�� | D�� | ��mg��1+$\frac{M}{m}$�� |
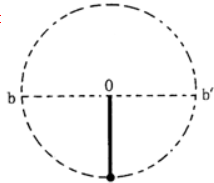 ��ͼ��һ��ΪL������ϸ��һ��������Ϊm��С����Ϊ�ʵ㣩��������һ�˿���O��ת������ʹ�����ͬһ��ֱ����������ת�������С������ļ��ٶȴ�СΪg��gΪ���ص��������ٶȣ�������˵����ȷ���ǣ�������
��ͼ��һ��ΪL������ϸ��һ��������Ϊm��С����Ϊ�ʵ㣩��������һ�˿���O��ת������ʹ�����ͬһ��ֱ����������ת�������С������ļ��ٶȴ�СΪg��gΪ���ص��������ٶȣ�������˵����ȷ���ǣ�������| A�� | С������ٶȴ�СΪgL | |
| B�� | С���˶�����ߵ�ʱ������ȫʧ��״̬ | |
| C�� | �����ת��ˮƽλ��ʱ����˶�С������������ָ��Բ��O | |
| D�� | ���������ת�������У���˶�С�������������ֵΪmg |
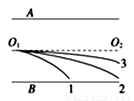
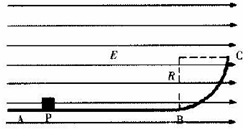 ��ͼ��ʾ���⻬����Ե��ˮƽ���AB���ķ�֮һԲ�����BCƽ�����ӣ���������ˮƽ���ҵ���ǿ�糡�У���֪��ǿ�糡�ij�ǿE=5��103V/m��Բ������뾶R=0.4m������һ������q=+2��10-5C������m=5��10-2kg����飨����Ϊ�ʵ㣩�Ӿ�B��s=1m����P���ɾ�ֹ�ͷţ������˶���B�ˣ���ƽ������Բ�����BC���������ٶ�g=10m/s2����
��ͼ��ʾ���⻬����Ե��ˮƽ���AB���ķ�֮һԲ�����BCƽ�����ӣ���������ˮƽ���ҵ���ǿ�糡�У���֪��ǿ�糡�ij�ǿE=5��103V/m��Բ������뾶R=0.4m������һ������q=+2��10-5C������m=5��10-2kg����飨����Ϊ�ʵ㣩�Ӿ�B��s=1m����P���ɾ�ֹ�ͷţ������˶���B�ˣ���ƽ������Բ�����BC���������ٶ�g=10m/s2����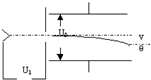 ��ͼ��ʾ�������ڵ��Ʋ�ΪU1�ļ��ٵ糡���ɾ�ֹ��ʼ�˶���Ȼ��������Ʋ�ΪU2������ƽ�н������ĵ糡�У��峤ΪL��������Ϊd�����䷽�������ƽ�У����Ƶ��������뿪ƫת�糡ʱ�IJ�λ��y��ƫת�ǦȵĹ�ϵ��
��ͼ��ʾ�������ڵ��Ʋ�ΪU1�ļ��ٵ糡���ɾ�ֹ��ʼ�˶���Ȼ��������Ʋ�ΪU2������ƽ�н������ĵ糡�У��峤ΪL��������Ϊd�����䷽�������ƽ�У����Ƶ��������뿪ƫת�糡ʱ�IJ�λ��y��ƫת�ǦȵĹ�ϵ��