题目内容
14.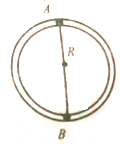 如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动,今对上方小球A施加微小扰动,两球开始运动后,下列说法正确的是( )
如图所示,半径为R的光滑细圆环轨道被固定在竖直平面上,轨道正上方和正下方分别有质量为2m和m的静止小球A、B,它们由长为2R的轻杆固定连接,圆环轨道内壁开有环形小槽,可使细杆无摩擦、无障碍地绕其中心点转动,今对上方小球A施加微小扰动,两球开始运动后,下列说法正确的是( )| A. | 轻杆转到水平位置时两球的加速度大小相等 | |
| B. | 轻杆转到竖直位置时两球的加速度大小不相等 | |
| C. | 运动过程中A球速度的最大值为$\sqrt{\frac{4gR}{3}}$ | |
| D. | 当A球运动到最低点时,两小球对轨道作用力的合力大小为$\frac{13}{3}$mg |
分析 本题的关键是明确球A与B组成的系统机械能守恒,球B减少的机械能应等于球A增加的机械能,通过球A减少的重力势能等于球B增加的重力势能和两球增加的动能之和即可求出球A的最大速度,再对A、B球应用牛顿第二定律和牛顿第三定律,可求出当A球运动到最低点时,两小球对轨道作用力的合力大小.
解答 解:A、轻杆转到水平位置时,AB的线速度大小相等,根据a=$\frac{{v}^{2}}{R}$,知两球在水平方向的向心加速度大小相等,两球在竖直方向的加速度方向相反,大小不等,故合加速度大小也不相等,故A错误.
B、轻杆转到竖直位置时,小球只受到竖直方向的合力,故只有向心加速度,两球的速度大小始终相等,根据a=$\frac{{v}^{2}}{R}$,可知,轻杆转到竖直位置时两球的加速度大小相等,故B错误.
C、两个球系统机械能守恒,当A球运动到最低点时,速度最大,有
2mg•2R-mg•2R=$\frac{1}{2}$(m+2m)v2,解得v=$\sqrt{\frac{4gR}{3}}$,故C正确.
D、在竖直位置时,设轨道对B球的弹力为FNB,轨道对A球的弹力为FNA
对B球 mBg+FNB=mB$\frac{{v}^{2}}{R}$,解得FNB=$\frac{1}{3}$mBg=$\frac{1}{3}$mg
对A球FNA-mAg=mA$\frac{{v}^{2}}{R}$,解得FNA=$\frac{14}{3}$mg
故轨道对AB两球的合力为F=FNA-FNB=$\frac{13}{3}$mg
根据牛顿第三定律,当A球运动到最低点时,两小球对轨道作用力的合力大小为$\frac{13}{3}$mg,故D正确.
故选:CD
点评 本题考查机械能守恒定律及牛顿第二定律的应用,要明确两球的速度大小相等,要知道小球通过最高点和最低点时由合力提供向心力.

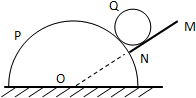 半圆柱体P放在粗糙的水平面上,有一挡板MN,其延长线总是过半圆柱体的轴心O,但挡板与半圆柱体不接触,在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态,如图是这个装置的截面图,若用外力使MN绕O点缓慢地逆时针转动,在Q到达最高位置前,发现P始终保持静止,在此过程中,下列说法正确的是( )
半圆柱体P放在粗糙的水平面上,有一挡板MN,其延长线总是过半圆柱体的轴心O,但挡板与半圆柱体不接触,在P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于静止状态,如图是这个装置的截面图,若用外力使MN绕O点缓慢地逆时针转动,在Q到达最高位置前,发现P始终保持静止,在此过程中,下列说法正确的是( )| A. | MN对Q的弹力大小保持不变 | B. | P、Q间的弹力先增大后减小 | ||
| C. | 桌面对P的摩擦力先增大后减小 | D. | P所受桌面的支持力一直增大 |
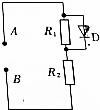 如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )
如图所示,电路中的电阻R1与电阻R2的阻值均为R,和R1并联的D为理想二极管(正向电阻可看作零,反向电阻可看作无穷大).在A、B间加某A一正弦交流电压时.则加在R2上的电压有效值为5$\sqrt{10}$V,由此可知这一正弦交流电压的最大值为( )| A. | 10V | B. | 10$\sqrt{2}$V | C. | 20V | D. | 20$\sqrt{2}$V |
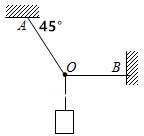 三段不可伸长的细绳OA、OB、OC共同悬挂一重物,如图所示,若重物的质量为100N,问OA、OB细绳的拉力分别为多大?
三段不可伸长的细绳OA、OB、OC共同悬挂一重物,如图所示,若重物的质量为100N,问OA、OB细绳的拉力分别为多大?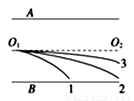
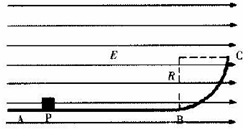 如图所示,光滑、绝缘的水平轨道AB与四分之一圆弧轨道BC平滑连接,并均处于水平向右的匀强电场中,已知匀强电场的场强E=5×103V/m,圆弧轨道半径R=0.4m.现有一带电量q=+2×10-5C、质量m=5×10-2kg的物块(可视为质点)从距B端s=1m处的P点由静止释放,加速运动到B端,再平滑进人圆弧轨道BC,重力加速度g=10m/s2,求:
如图所示,光滑、绝缘的水平轨道AB与四分之一圆弧轨道BC平滑连接,并均处于水平向右的匀强电场中,已知匀强电场的场强E=5×103V/m,圆弧轨道半径R=0.4m.现有一带电量q=+2×10-5C、质量m=5×10-2kg的物块(可视为质点)从距B端s=1m处的P点由静止释放,加速运动到B端,再平滑进人圆弧轨道BC,重力加速度g=10m/s2,求: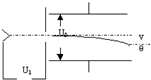 如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行金属板间的电场中,板长为L,板间距离为d,入射方向跟极板平行,试推导出电子离开偏转电场时的侧位移y和偏转角θ的关系.
如图所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行金属板间的电场中,板长为L,板间距离为d,入射方向跟极板平行,试推导出电子离开偏转电场时的侧位移y和偏转角θ的关系.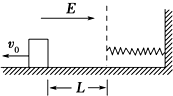 在绝缘水平面上放有一带正电的滑块、质量为m,带电荷量为q,水平面上方虚线左侧空间有水平向右的匀强电场,场强为E,qE>μmg,虚线右侧的水平面光滑.一轻弹簧右端固定在墙上,处于原长时,左端恰好位于虚线位置,把滑块放到虚线左侧L处,并给滑块一个向左的初速度v0,已知滑块与绝缘水平面间的动摩擦因数为μ,求:
在绝缘水平面上放有一带正电的滑块、质量为m,带电荷量为q,水平面上方虚线左侧空间有水平向右的匀强电场,场强为E,qE>μmg,虚线右侧的水平面光滑.一轻弹簧右端固定在墙上,处于原长时,左端恰好位于虚线位置,把滑块放到虚线左侧L处,并给滑块一个向左的初速度v0,已知滑块与绝缘水平面间的动摩擦因数为μ,求: