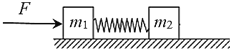
��Ŀ����
����Ŀ����ͼ��ʾ���⻬��ˮƽ��������һ����ΪM=2kg������ΪL=2m��ľ�壬ľ���Ҷ���һ����Ϊm=1kg��С��飬��ʼʱ���Ǿ���ֹ����֪����ľ���Ķ�Ħ������Ϊ![]() ��ȡ�������ٶ�Ϊ
��ȡ�������ٶ�Ϊ![]() �����Ħ�����ͻ���Ħ������С����Ϊ��ȡ�
�����Ħ�����ͻ���Ħ������С����Ϊ��ȡ�
��1������ľ��ʩ��ˮƽ���ҵĺ���F��ʹľ���ܴ�����������������F�Ĵ�СӦ����ʲô������
��2�����ָ�ľ��ʩ��ˮƽ���ҵ�����![]() ����
����![]() ʱ�䣬Ȼ��
ʱ�䣬Ȼ��![]() ���Ϊ����ˮƽ���ҡ���СΪ2N������
���Ϊ����ˮƽ���ҡ���СΪ2N������![]() ������ľ�岻�ܴ�����³����������
������ľ�岻�ܴ�����³����������![]() �Ĵ�С�����������
�Ĵ�С�����������

���𰸡�(1) F >6N,(2) ![]() .
.
�����������������ΪʹС�����ľ���ϵ��£���С���������ľ�廬���������С�����������������ٽ���ٶȣ��ٶ��������������ţ�ٵڶ������������F����Сֵ������ţ�ٵڶ��������ˮƽ����ΪF1ʱľ���ľ��ļ��ٶ�����ˮƽ����ΪF2ʱ��ľ�����ܺ�����Ϊ�㣬��ʼ������ֱ���˶�ֱ��������ٶ���ȣ��ڽ���˶�ѧ��ʽ��λ�Ƽ�Ĺ�ϵ����������������������
����ľ��ʩ��ˮƽ���ҵĺ���Fʱ����ľ����������ļ��ٶȴ�С�ֱ�Ϊa1��a2
��ţ�ٵڶ������У���ľ�壺F����mg=Ma1
����飺��mg=ma2
Ҫʹľ���ܴ������������Ӧ����a1> a2
�������ϲ��������ݿɵ���F >6N
(2)���ľ��ʩ��ˮƽ���ҵ�����F1ʱ��ľ���������黬������ʱ������ԣ�1���еļ��ٶ�a2=ug�����˶�����ľ��ļ��ٶȴ�СΪa3��t1ʱ��������ٶ�Ϊv��λ��Ϊs1
��ľ����ţ�ٵڶ������У�F1����mg=Ma3
�����˶�ѧ�����У�v=a3t1�� s1=![]() t1
t1
��ˮƽ����ΪF2ʱ��ľ�����ܺ�����Ϊ�㣬��ʼ������ֱ���˶�ֱ��������ٶ���ȣ���ù�����ľ���λ��Ϊs2���������һ�����ȼ����˶������ǵ�v-tͼ����ͼ��ʾ��

���˶�ѧ�����У�s2=v(t2-t1)
�����Ӿ�ֹ���ٵ�v����ʱ��Ϊt2��λ��Ϊs3�����˶�ѧ�����У�v=a2t2��s3![]() t2
t2
Ҫ����ľ�岻�ܴ�����³������s1+s2��s3+L
�������ϲ��������ݿɵã�F1��10N

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�