��Ŀ����
����Ŀ����ͼ��ʾ��O��Ϊ���ģ�����1���Ƶ��������������˶�������2���Ƶ������еĹ��Ϊ��Բ�����������ͬһƽ���ڡ���֪Բ�����ֱ��������Բ����ij��ᣬ�ҵ���λ����Բ�����һ�������ϣ���������ΪG�����������ΪM������1�Ĺ���뾶ΪR��OQ=1.5R������˵����ȷ����
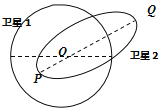
A.����1���������ڴ�������2����������
B.����2�� P��Q����ٶȴ�С��ϵΪ![]()
C.����2��Q ����ٶ�![]()
D.�������1�ļ��ٶ�Ϊa������2��P��ļ��ٶ�Ϊa p ���� a��ap
���𰸡�CD
��������
A���ɿ����յ������ɿɵã�
![]()
��֪Բ����İ뾶������Բ����İ볤�ᣬ�������ǵ�����������ȣ���A����
B������2����Բ�˶�����λʱ���ڣ����Ǻ͵�������ɨ���������ȣ���P������2�͵������߳���С����Q������2�͵������ߵij��ȣ�����![]() ��B����
��B����
C�������֪����2��Q�㿪ʼ�������˶����������2�ڹ�Q��ʱ������������������������
![]()
���
![]()
C��ȷ��
D�����������й�����ֻ�������������ã����У�
![]()
���Լ��ٶ�
![]()
�������֪��OP=0.5R<R������a<aP����D��ȷ��

��ϰ��ϵ�д�
�����Ŀ