题目内容
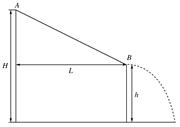
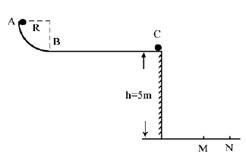
(12分)如图所示,水平轨道CD与光滑竖直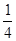 圆轨道ED、BC分别相切于D、C点。质量m=2kg的小滑块从圆轨道B点上方由静止释放,通过B点切如轨道BC,此后,滑块在轨道内往复运动。已知AB间高度差h=1.6m,圆轨道半径均为R=1.6m,CD长l=3.5m,滑块与CD间的动摩擦因数
圆轨道ED、BC分别相切于D、C点。质量m=2kg的小滑块从圆轨道B点上方由静止释放,通过B点切如轨道BC,此后,滑块在轨道内往复运动。已知AB间高度差h=1.6m,圆轨道半径均为R=1.6m,CD长l=3.5m,滑块与CD间的动摩擦因数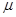 =0.4,取g=10m/s2,求:
=0.4,取g=10m/s2,求:
(1)滑块落入轨道后,能离开水平轨道CD的最大高度;
(2)滑块最终停在距C点多远处;
(3)滑块在水平轨道CD上运动的总时间。
(1)H=1.8m(2)s=8m(3)t="2s"
解析试题分析:(1)滑块第一次滑过CD后上升的高度最大,设为H,由动能定理:
mg(h+R)- 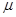 mgl+mgH=0 ①
mgl+mgH=0 ①
解得:H=1.8m ②
(2)滑块在水平轨道上滑动的路程为s,由能量守恒: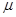 mgs=mg(h+R) ③
mgs=mg(h+R) ③
解得:s=8m ④
故滑块停在距C点1m处 ⑤
(3)滑块第一次到达C的速度v满足:mg(h+R)=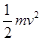 ⑥
⑥
滑块在CD段上的往复运动可等效为一个单方向的匀减速直线运动
0=v-at ⑦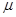 mg=ma ⑧
mg=ma ⑧
解得:t=2s ⑨
评分标准:本题共12分,①②③每式2分,其余每式1分
考点:动能定理匀减速直线运动

关于重力做功和重力势能,下列说法正确的是
| A.重力做功与物体运动的路径有关 |
| B.重力对物体做负功时,物体的重力势能一定减小 |
| C.重力势能为负值说明物体在零势能面以下 |
| D.重力势能的变化与零势能面的选取有关 |
如图甲所示,abcd是位于竖直平面内的正方形闭合金属线框,金属线框的质量为m,电阻为R。在金属线框的下方有一匀强磁场区域,MN和M′N′是匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直。现金属线框由距MN的某一高度从静止开始下落,图乙是金属线框由开始下落到完全穿过匀强磁场区域瞬间的速度-时间图象,图象中坐标轴上所标出的字母均为已知量。可知
| A.金属框初始位置的bc边到边界MN的高度为v1t1 |
B.金属框的边长为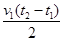 |
C.磁场的磁感应强度为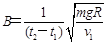 |
| D.在进入磁场过程中金属框产生的热为mgv1(t2-t1) |

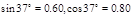 )求:
)求:

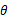 。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件
。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件 。
。
 ).求:
).求: