题目内容
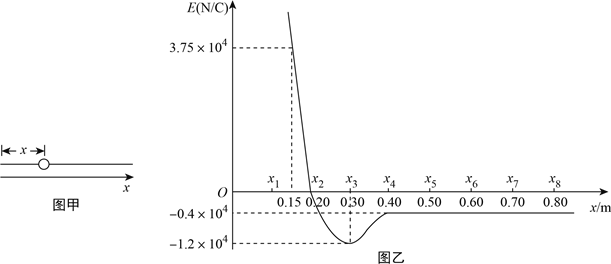
【题目】如图甲所示,光滑的绝缘细杆水平放置,有孔小球套在杆上,整个装置固定于某一电场中.以杆左端为原点,沿杆向右为![]() 轴正方向建立坐标系.沿杆方向电场强度
轴正方向建立坐标系.沿杆方向电场强度![]() 随位置
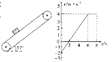
随位置![]() 的分布如图乙所示,场强为正表示方向水平向右,场强为负表示方向水平向左.图乙中曲线在
的分布如图乙所示,场强为正表示方向水平向右,场强为负表示方向水平向左.图乙中曲线在![]() 和
和![]() 范围可看作直线.小球质量
范围可看作直线.小球质量![]() ,带电量
,带电量![]() .若小球在
.若小球在![]() 处获得一个
处获得一个![]() 的向右初速度,最远可以运动到
的向右初速度,最远可以运动到![]() 处.
处.
(1)求杆上![]() 到
到![]() 两点间的电势差大小比
两点间的电势差大小比![]() ;
;
(2)若小球在![]() 处由静止释放后,开始向左运动,求:
处由静止释放后,开始向左运动,求:
a.加速运动过程中的最大加速度![]() ;
;
b.向左运动的最大距离
(3)若已知小球在![]() 处以初速度
处以初速度![]() 向左减速运动,速度减为零后文又返
向左减速运动,速度减为零后文又返![]() 处,所用总时间为
处,所用总时间为![]() ,求小球在
,求小球在![]() 处以初速度
处以初速度![]() 向左运动,再返回到
向左运动,再返回到![]() 处所用的时间(小球运动过程中始终末脱离杆).你可能不会计算,但小球向左运动过程中受力特点你并不陌生,请展开联想,通过类比分析得出结果.
处所用的时间(小球运动过程中始终末脱离杆).你可能不会计算,但小球向左运动过程中受力特点你并不陌生,请展开联想,通过类比分析得出结果.
【答案】(1)![]() (2)a.
(2)a. ![]() b.
b. ![]() .(3)见解析
.(3)见解析
【解析】(1)![]() 与
与![]() 之间为匀强电均的电场强度为
之间为匀强电均的电场强度为![]() ,
, ![]() ;
;
(2)a.加速运动过程中,经过![]() 处场强最大,为
处场强最大,为![]() ,
,
由牛顿第二定律有: ![]() ,得
,得![]()
b.设![]() 与
与![]() 之间的电势差为
之间的电势差为![]() ,由动能定理有:
,由动能定理有: ![]()
得: ![]() ;
;
设![]() 与
与![]() 之间的电势差为:
之间的电势差为: ![]()
设向左运动的最远处距![]() 处的距离为
处的距离为![]() ,电场强度大小为
,电场强度大小为![]() ,带电小球由位置
,带电小球由位置![]() 处到最远处的过程,根据动能定理:
处到最远处的过程,根据动能定理: ![]() ,
, ![]() ,
,
得![]() ,所以
,所以![]() 。
。
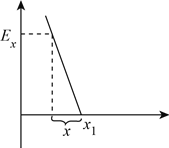
(3)如图:设距![]() 处左侧距离为
处左侧距离为![]() 处的电场强度大小为
处的电场强度大小为![]()
小球在距![]() 处左侧距离为
处左侧距离为![]() 处所受电场力大小为F,则
处所受电场力大小为F,则![]()
由图可以知道: ![]() (
(![]() 为常量),所以
为常量),所以![]()
小球在![]() 处左侧所受电场力方向总指向
处左侧所受电场力方向总指向![]() (向右)
(向右)
小球在![]() 处左侧相对于
处左侧相对于![]() 处的位移总背离
处的位移总背离![]() (向左)
(向左)
综上可知,电场力![]() 的大小与
的大小与![]() 成正比,方向与
成正比,方向与![]() 方向相反,小球向左的运动是简谐运动的一部分,振动周期与振幅无关,小球从
方向相反,小球向左的运动是简谐运动的一部分,振动周期与振幅无关,小球从![]() 处向左运动再返回的时间是简谐运动的半个周,此以
处向左运动再返回的时间是简谐运动的半个周,此以![]() 为初速度的时间仍为
为初速度的时间仍为![]() 。
。

练习册系列答案
相关题目