Question

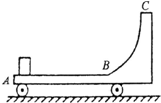
一个物体从斜面上高h处由静止滑下并紧接着在水平面上滑行一段距离后停止，量得停止处到开始运动处的水平距离为s（如图所示），不考虑物体滑至斜面底端的碰撞作用，并认为斜面与水平面对物体的动摩擦因数相同，求动摩擦因数μ．

Answer 1

对物体全过程应用动能定理，有mgh-μmgcosθ.

h

sinθ

-μmg(s-

h

tanθ

)=0，解得μ=

h

s

．
即动摩擦因数μ为

h

s

．
（本题也可直接利用结论：物体沿斜面下滑过程中克服摩擦力做的功等于动摩擦因数、重力以及斜面底边长三者的乘积．证明如下：设斜面长L，斜面倾角为θ，由于物体受到的滑动摩擦力为f=μmgcosθ，所以物体克服摩擦力做功为

W

克

=fL=μmgcosθ．L，因为斜面底边长为s=Lcosθ，所以

W

克

=μmgs，得证．所以本题可直接这样由动能定理mgh-μmgs=0，解得μ=

h

s

）