Question

【题目】如图，L1、L2 为地月系统的两个拉格朗日点，卫星位于这两点时，会在地球引力与月球引力的共同作用下，可以 几乎不消耗燃料而保持与月球同步绕地球做圆周运动。若 有两颗质量相同的卫星分别位于 L1、L2，则

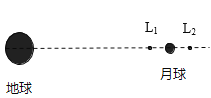
A. 在 L2 处的卫星的角速度大于在 L1 处的

B. 在 L2 处的卫星的线速度大于在 L1 处的

C. 在 L2 处的卫星的向心加速度大于在 L1 处的

D. 在 L2 处的卫星受到的地球引力大于在 L1 处的

Answer 1

【答案】BC

【解析】

两星保持与月球同步绕地球做圆周运动，则角速度相同，根据v=ωr可知线速度关系；根据a=ω2r可知向心加速度关系；根据万有引力定律可判断受地球的引力关系。

根据题意可知，两颗卫星位于L1处和L2处时绕地球运动的角速度都与月球绕地球运转的角速度相同，根据v=ωr可知，在 L2 处的卫星的线速度大于在 L1 处的，选项A错误，B正确；根据a=ω2r可知，在 L2 处的卫星的向心加速度大于在 L1 处的，选项C正确；根据万有引力定律可知在 L2 处的卫星受到的地球引力小于在 L1 处的，选项D错误；故选BC.