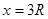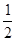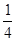题目内容
如图甲所示,一轻弹簧的两端与质量分别为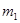 和
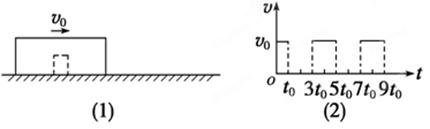
和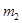 的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得
的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得
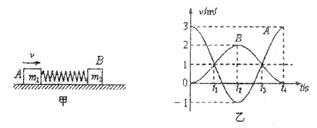
A. 在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B. 从t3到t4时刻弹簧由压缩状态恢复到原长
C. 两物体的质量之比为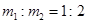
D. 在t2时刻A与B的动能之比为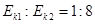
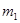 和
和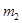 的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得
的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得
A. 在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B. 从t3到t4时刻弹簧由压缩状态恢复到原长
C. 两物体的质量之比为
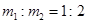
D. 在t2时刻A与B的动能之比为
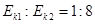
CD
试卷分析:对于整体由于无摩擦,因此整体受力为零,系统动量守恒且机械能守恒。在0~t1内由于A的速度大于B的速度,所以弹簧正在压缩中,此后弹簧将B弹开使之继续加速,而对A向左,使其继续减速。由于在(t2~t3)时间内,B物体速度大于A的速度,所以弹簧一直伸长,所以t3时刻应该是弹簧伸长最长时,所以A错。接下来弹簧开始缩短,A加速,B减速,所以B错误。根据动量守恒定律
 ,所以
,所以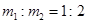 ,C正确。因为在t2时刻,a、b物体速度均知道,所以可以求得
,C正确。因为在t2时刻,a、b物体速度均知道,所以可以求得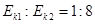 ,所以D正确。
,所以D正确。点评:此类题型考察了动量守恒定律约束下的物体的运动,并结合两物体的运动特点转化为它们的v-t图像,通过分析其运动找到两物体间的间距。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目