题目内容
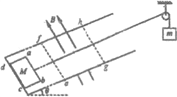
【题目】如图所示,粗糙的水平桌面上有一轻弹簧,左端固定在A点,水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量m=0.2kg的物块将弹簧缓慢压缩到C点,弹簧和物块具有的弹性势能为Ep,释放后物块从桌面右边缘D点飞离桌面后,由P点沿圆轨道切线落入圆轨道。已知物块与桌面间动摩擦因数μ=0.1,CD间距离SCD=0.5m。(g=10m/s2),求:
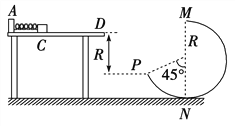
(1)D点的速度vD;
(2) Ep的大小
(3)判断m能否沿圆轨道到达M点。
【答案】(1)4m/s(2)1.8J(3)物块不能到达M点
【解析】(1)设物块由D点以初速度vD做平抛运动,落到P点时其竖直速度为vy,有![]()
![]() ,
,
得vD=4m/s
(2)物块从C→D由动能定理得:-μmgSCD=![]() mvD2-
mvD2-![]() mvC2
mvC2
功能关系:Ep=![]() mv2C=1.8J
mv2C=1.8J
(3)设物块能沿轨道到达M点,其速度为vM,从D→M整个过程由机械能守恒定律得:
![]() mvD2=
mvD2=![]() mvM2+mgR·cos45°
mvM2+mgR·cos45°
代入数据解得:vM≈2.2m/s<![]() ≈2.8m/s
≈2.8m/s
所以物块不能到达M点.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目