题目内容
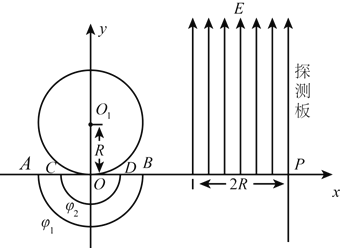
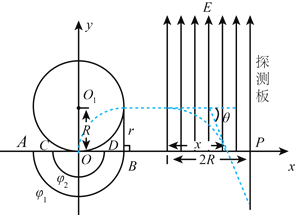
【题目】如图所示，在直角坐标系xOy中，有一沿半径方向的加速电场区域，AB、CD为加速电场的两个同心半圆弧边界，圆心为O，外圆弧面AB电势为φ1，内圆弧面CD电势为φ2。在x轴上方有一与x轴相切的半径为R的圆形匀强磁场区域，磁场方向垂直于纸面向里（未画出），圆心在y轴上O1处。在圆形磁场右侧的第一象限中存在着宽度为2R的匀强电场，方向沿y轴正方向，电场右边界存在着与y轴平行的足够长的探测板，与x轴相交于P点。假设质量为m，电荷量为q的带负电的粒子能均匀地吸附在AB圆弧上，并被加速电场从静止开始加速聚焦于原点O并进入圆形磁场，发现所有带电粒子出磁场时均平行于x轴正方向，后进入匀强电场并最终打在探测板上，并且从y轴正方向射入圆形磁场的粒子正好打在探测板的P点上。求：
（1）粒子被加速电场加速后的速度大小和圆形匀强磁场B的大小；
（2）匀强电场E的大小；
（3）粒子打在探测板上的范围。
【答案】（1）
；
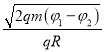（2）
（3）-
【解析】
设在加速电场中加速后到达O点的速度为v0，由动能定理：
解得
由于出圆形磁场后的粒子速度方向均平行于x轴正方向，因此带电粒子在磁场中的轨迹圆半径等于磁场半径
解得
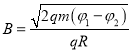
（1）从y轴负方向进入O点的粒子在y=R处离开磁场做匀速直线运动，到达电场后做类平抛运动到达P点：
解得
（2）带电粒子进入匀强电场后做类平抛运动，之后做匀速直线运动，知y=2R出射的粒子打在探测板上y=R处，y<R的出射的粒子打在P点下方的探测板上，设距x轴上方L(0<L<R)处出射的粒子打在探测板P点下方的距离为H，如图所示：
联立可得
将H对L求导，并令其等于0，得极值点
因此粒子打在探测板上的范围
练习册系列答案
相关题目
