题目内容
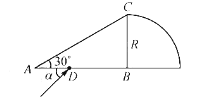
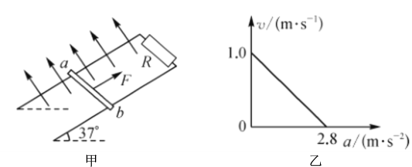
【题目】如图所示,水平面上固定一倾角为![]() =37°的斜面体,在其左侧一定距离有一水平桌面,现将一可视为质点的物块A由水平桌面的左端以初速度v0=6m/s向右滑动,滑到右端时与物块B发生弹性碰撞,物块B离开桌面后,经过一段时间,刚好无碰撞地由光滑固定的斜面体顶端C点滑上斜面体已知桌面两端之间的距离为x=4.0m,mB=1kg,物块A与水平桌面之间的动摩擦因数为μ=0.25,桌面与斜面体C点的高度差为h=0.45m,重力加速度取g=10m/s2,sin 37°=0.6,cos 37°=0.8,忽略空气阻力。求:
=37°的斜面体,在其左侧一定距离有一水平桌面,现将一可视为质点的物块A由水平桌面的左端以初速度v0=6m/s向右滑动,滑到右端时与物块B发生弹性碰撞,物块B离开桌面后,经过一段时间,刚好无碰撞地由光滑固定的斜面体顶端C点滑上斜面体已知桌面两端之间的距离为x=4.0m,mB=1kg,物块A与水平桌面之间的动摩擦因数为μ=0.25,桌面与斜面体C点的高度差为h=0.45m,重力加速度取g=10m/s2,sin 37°=0.6,cos 37°=0.8,忽略空气阻力。求:
(1)物块A的质量;
(2)如果斜面体C点距离水平面的高度为H=4.8m,求从物块A开始运动到物块B到达D点的总时间。

【答案】(1)1kg;(2)2.1s。
【解析】
(1)由平抛运动规律,物块B离开桌面后在竖直方向做自由落体运动,则有
![]()
代入数据解得![]() =0.3s
=0.3s
竖直方向速度
![]() 3m/s
3m/s
根据几何关系,可知此时速度与水平速度的夹角等于斜面的倾角,即![]() =37°,则有
=37°,则有
![]()
解得物块B离开桌面时速度为![]() m/s
m/s
设滑块在平台上滑动时的加速度为a,滑块到达B点的速度![]() ,根据牛顿第二定律有
,根据牛顿第二定律有
![]()
解得![]() m/s2
m/s2
根据速度位移公式有
![]()
解得![]() m/s
m/s
根据动量守恒得
![]()
根据机械能守恒得
![]()
代入数据解得![]() ,
,![]() kg
kg
(2)物块A在水平桌面上运动的时间为
![]() s
s
物块B到达斜面体C点的合速度为
![]()
代入数据解得v=5m/s
物块B在斜面上运动时,根据牛顿第二定律有
![]()
代入数据解得加速度![]() m/s2
m/s2
根据几何关系,有斜面的长度
![]() m=0.8m
m=0.8m
根据运动学公式有
![]()
解得![]() 1s(
1s(![]() s舍去)
s舍去)
从物块A开始运动到物块B到达D点的总时间
![]() s
s

练习册系列答案
相关题目